Задания. Вязкость пластичной жидкости находится по следующей формуле:

Варианты 1.1 – 1.3

Вязкость пластичной жидкости находится по следующей формуле:

,

где t₀ – напряжение внутреннего трения, при котором пластичная жидкость начинает движение, Н/м²; d – диаметр проходного сечения, м; w- средняя скорость жидкости, м/c; h – коэффициент пропорциональности, характеризующий пластичные свойства жидкости.

Определить t₀ и h, если известно, что d= 0.2 м и в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные	Метод решения системы линейных уравнений
i
1.1	w	0.2	0.25	0.4	0.6	0.7	0.75	0.9	-	Крамера
m								-
1.2	w	0.3	0.4	0.7	0.9	1.2	1.4	1.5	1.7	Гаусса
m
1.3	w	0.25	0.5	0.6		1.5		2.75		Обращения матриц
m

 

Варианты 1.4 – 1.6

Эффективную скорость газа, соответствующую началу подвисания жидкости при прохождении газа через нее, можно найти по числу Рейнольдса, определяемого по формуле:

,

где Ar – критерий Архимеда, соответствующий эквивалентному диаметру насадки и плотности газа; W_g и W_f – скорости газа и жидкости, кг/ч; a и b – константы.

Определить a и b, если известно, что W_g =12300 кг/ч, Ar=46 и в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные	Метод решения системы линейных уравнений
i
1.4	Wf									Обращения матриц
Re
1.5	Wf								-	Гаусса
Re								-
1.6	Wf							-	-	Крамера
Re							-	-

 

Варианты 1.7 – 1.9

Постоянная составляющая помехи в электрической сети описывается следующей математической моделью:

где w₁ и w₂ – угловые скорости, рад/с; t – время, с; U – напряжение, В; a₀, a₁, a₂ – константы.

Определить a₀, a₁, a₂, если известно, что w₁=5 рад/с, w₂=10 рад/с и в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные	Метод решения системы линейных уравнений
i
1.7	t	0.1	0.5	0.6	0.8	1.1	1.4	1.6	1.8	Обращения матриц
U			-16	-5			-2	-20
1.8	t	0.2	0.3	0.5	0.8	0.9		1.2	1.4	Гаусса
U
1.9	t	0.1	0.2	0.4	0.8	0.9		1.2	1.5	Крамера
U	3.2	3.3	2.7	3.1	3.05	2.9		3.2

 

 

Варианты 1.10 -1.13

Изменение температуры в зависимости от времени в трубчатом реакторе можно описать следующей математической моделью:

,

где t – время, с; Т - температура реакционной массы, К; a₀, a₁, a₂ – константы.

Определитьa₀, a₁, a₂, если известно, что в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные	Метод решения системы линейных уравнений
i
1.10	t								-	Крамера
T
1.11	t									Обращения матриц
T			300.5	300.5
1.12	t									Гаусса
T
1.13	t							-	-	Обращения матриц
T							-	-

 

Варианты 2.1 -2.3

Константа скорости химической реакции подчиняется закону Аррениуса:

,

где k₀ – постоянная скорости химической реакции; Т – температура реакционной массы, К; E – энергия активации, кДж/моль; R= 8.32 универсальная газовая постоянная, кДж/(К× моль).

Определить k₀ иE, если известно, что в ходе исследования получены следующие экспериментальные данные:

 

Номер варианта	Экспериментальные данные	Метод решения системы линейных уравнений
i
2.1	T	277.5						297.5	-	Обращения матриц
K			1239.5		1239.8	1240.5		-
2.2	T						292.5			Гаусса
K
2.3	T								-	Крамера
K								-

 

Варианты 2.4 -2.9

Зависимость максимальной ньютоновской вязкости полимера в растворе без учета средневязкостного молекулярного веса и коэффициента полидисперсности полимера выглядит следующим образом:

,

где Т – температура реакционной массы, К; R= 8.32 универсальная газовая постоянная, кДж/(К× моль); C_p – концентрация полимера, безразм.; a1, a2, a3, – константы; А – поправочный коэффициент ед. измерения, Па× с.

а) Определить значения констант a1, a2, a3при Т= 300 К, А = 0.51 Па× с, если известны следующие экспериментальные данные

 

Номер варианта	Экспериментальные данные	Метод решения системы линейных уравнений
i
2.4	Cp	0.05	0.2	0.4	0.6	0.8	0.9	0.95	-	Гаусса
h0	0.1	0.3	0.6	0.9	1.2	1.5	1.5	-
2.5	Cp	0.1	0.2	0.3	0.4	0.7	0.8	0.9	-	Крамера
h0		3.5	5.1		8.5		9.4	-
2.6	Cp	0.05	0.15	0.3	0.4	0.5	0.6	0.7	0.9	Обращения матриц
h0

 

б) Определить значения констант Аиa3при C_p = 0.5, a1=1.9, a2=2.7, если известны следующие экспериментальные данные

Номер варианта	Экспериментальные данные	Метод решения системы линейных уравнений
i
2.7	Т									Крамера
h0				3.5			1.8
2.8	Т								-	Обращения матриц
h0								-
2.9	Т								-	Гаусса
h0							13.5	-

 

Варианты 2.10 – 2.13

Постоянная составляющая помехи в электрической сети описывается следующей математической моделью:

,

где w₁ – угловая скорость, рад/с; t – время, с; U – напряжение, В; a₀, a₁, a₂ – константы.

Определить a₀, a₁, a₂, если известно, что w₁=15 рад/с и в ходе исследования получены следующие экспериментальные данные:

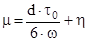Номер варианта	Экспериментальные данные	Метод решения системы линейных уравнений
	i
2.10	t	0.05	0.15	0.2	0.3	0.7	0.8	0.85	0.9	Крамера
U				-5
2.11	t	0.1	0.15	0.2	0.3	0.4	0.5	0.55	-	Гаусса
U								-
2.12	t	0.05	0.1	0.25	0.4	0.6	0.65	0.8	-	Крамера
U	-7	-3						-
2.13	t		0.2	0.3	0.4	0.5	0.6	0.7		Обращения матриц
U