Метод средних
Параметры a1 a2 ¼, ak аппроксимирующей зависимости (12) находятся, исходя из следующего условия (сумма невязок между экспериментальными и расчетными данными на всем интервале аппроксимации должна быть равна нулю, рис. 28):
где yiэ – экспериментальные данные;
i – порядковый номер точки;
m – число экспериментальных точек. Рис. 28. Метод средних (ye – экспериментальные данные, ysr – расчетные данные) Невязкой называется разница между экспериментальным и расчетным значением. В зависимости от взаимного положения экспериментальной и расчетной кривой, одни невязки положительны, а другие отрицательны. Но в целом расчетная кривая должна пройти так, чтобы невязки в сумме давали нуль. Для примера выберем ту же зависимость (13)
Необходимо найти неизвестные параметры a0 a1, a2. Для этого все измерения, заданные в табл. 6, разбиваются на группы, обычно равные. Количество групп равно количеству неизвестных параметров, т. е. k. Обозначим M как целую часть от деления:
Для данной аппроксимирующей зависимости М примерно равно m/ 3, таблица экспериментальных данных разбивается на три группы. Тогда для каждой группы, исходя из условия (17), можно записать уравнения:
или
Решение полученной системы уравнений (18) относительно неизвестных параметров a0, a1, a2 позволяет найти параметры аппроксимирующей зависимости. Теперь применим метод средних для нахождения параметров зависимости (15)
Как и в предыдущем методе, приведем зависимость (15) к линейному виду относительно неизвестных коэффициентов и получим
Тогда вместо зависимости (17)
в качестве условия поиска коэффициентов используем
или
Разобьём экспериментальную табл. 6 на 3 группы, для каждой группы, исходя из условия (19), получим систему линейных уравнений:
или
Решаем систему (20) относительно А0, a1, a2. Затем рассчитаем коэффициент а0:
|

 , (17)
, (17) – расчетные данные;
– расчетные данные;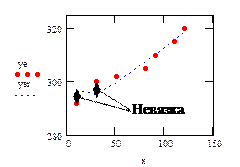
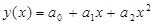 .
.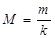 .
.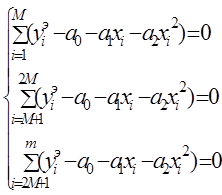
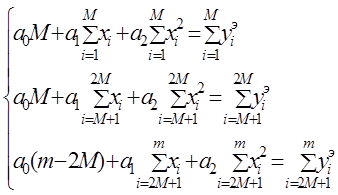 (18)
(18)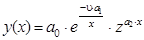 .
. .
.
 . (19)
. (19)
 (20)
(20)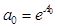 .
.


