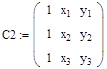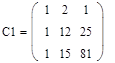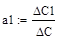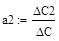Интерполирование степенными многочленами с использованием метода неопределенных коэффициентов
Запрограммируем в Mathcad решение примера 1. 1. Задаем системной переменной значение 1.
2. Задаем начальные значения экспериментальных массивов согласно табл. 3.
3. Задаем значение контрольной точки аргумента, в которой надо найти значение искомой функции: 4. Строим график экспериментальных значений (рис. 24).
Рис. 24. График экспериментальных значений 5. Так как имеем три экспериментальных точки, в качестве интерполирующей зависимости выберем степенной многочлен 2-го порядка
Пользуясь полученной формулой, составим систему линейных уравнений:
Данную систему запишем в векторно-матричной форме:
или
6. Решим полученную систему методом Крамера. Для этого сформируем 4 матрицы. Первая матрица С – главная матрица системы, остальные матрицы С0, С1 и С2 получаются из матрицы С путем замены 1-го, 2-го и 3-го столбца на вектор
Следует отметить, что программирование осуществляется с использованием имен переменных, а не значений. Это позволит сделать программу универсальной и использовать её для решения других подобных задач в дальнейшем. Далее контролируем заполнение матриц:
7. Осуществляем расчет определителя матрицы С согласно правилу миноров. Для набора формулы используем панель Greek (Греческий алфавит) и Matrix (Матрицы). Следует учесть, что для обозначения элементов двумерной матрицы С используется два индекса, разделенных запятыми (первый нумерует строку, второй – столбец). Если формула выходит за пределы страницы документа, часть её необходимо подсветить
и нажать Ctrl+Enter. В результате формула разобьётся на две строки.
Если удалить подсвеченный красным местозаполнитель, формула будет рассчитываться автоматически, как и прежде.
Далее высвечиваем результат расчета
и осуществляем проверку нажатием кнопки Determinant (Вычисление определителя) на панели Matrix (Матрицы)
Аналогично осуществляем расчет и проверку расчета определителей матриц С0, С1 и С2. 8. Рассчитываем коэффициенты a0, a1, a2.
9. Используя найденные коэффициенты, задаем функцию yr(xk) для получения расчетных значений. Имя функции отличается от y(x), чтобы не испортить заданные в начале программы значения экспериментальных массивов x и y.
Высвечиваем расчетное значение функции в контрольной точке (как и ожидалось, оно находится между второй и третьей экспериментальными токами – 12 и 15):
10. Добавляем к построенному ранее графику экспериментальных значений расчетную кривую yr(x1). Для этого сначала вводим ранжированную переменную x1, которая позволит получить не три, а девять расчетных значений и построить более гладкий график функции, отраженный с помощью пунктирной линии (рис. 25). Значение контрольной точки отражаем на графике с помощью крестика.
Рис. 25. Графики, полученные при интерполировании методом неопределенных коэффициентов
|



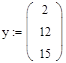


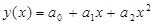 .
.

 .
. соответственно.
соответственно.