Краткие теоретические сведения. На практике очень часто зависимости между интересующими нас величинами задаются таблично, например, зависимость между температурой и ЭДС термопары задается в
На практике очень часто зависимости между интересующими нас величинами задаются таблично, например, зависимость между температурой и ЭДС термопары задается в виде градуировочных таблиц. В случае задания зависимости в виде таблицы нет возможности определения значений, находящихся между табличными значениями. Для решения данной задачи необходимо заменить таблично заданную зависимость аналитической зависимостью. Математическая постановка задачи интерполирования Пусть дана табличная зависимость
i= 1, 2, …, m, где n=m-1 – порядок fn(xi). Шагом интерполирования называется величина h, определяемая следующим соотношением:
Величина h может быть на всем рассматриваемом интервале постоянной (равностоящая интерполяция) и непостоянной (неравностоящая интерполяция). Значения f(xi) называются узлами интерполирования. Положим, что
есть произвольная функциональная зависимость, в общем случае нелинейная относительно неизвестных коэффициентов a0, a1, ¼, an (число определяемых коэффициентов в общем случае не должно быть меньше числа экспериментальных точек). Тогда задача интерполирования заключается в определении указанных коэффициентов исходя из условия (3) и нахождении межтабличных значений с использованием этой зависимости. Рассмотрим функциональную зависимость, линейную относительно коэффициентов a0, a1, ¼, an. Одним из распространенных классов функций, используемых при интерполировании, является класс многочленов. Рассмотрим степенные многочлены. Функция f(x) при этом принимается в виде:
При интерполировании многочленами число определяемых коэффициентов должно быть равно числу экспериментальных точек.
|

 (табл. 2), где m – число экспериментальных точек.
(табл. 2), где m – число экспериментальных точек.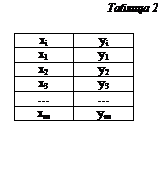 Необходимо найти такую зависимость y=fn(x), для которой все значения в узлах интерполирования совпадают с табличными
Необходимо найти такую зависимость y=fn(x), для которой все значения в узлах интерполирования совпадают с табличными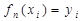 (3)
(3) .
.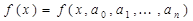 (4)
(4) . (5)
. (5)


