Интерполяционный многочлен Лагранжа. Интерполяционный многочлен Лагранжа, принимающий значения y1, , yn+1 в соответствующих точках, записывается в виде:Интерполяционный многочлен Лагранжа, принимающий значения y1, …, yn+1 в соответствующих точках, записывается в виде:
или
Интерполяционный многочлен Лагранжа можно построить при любом расположении узлов интерполирования (точки могут быть не равностоящие). Однако его недостатком является то, что при изменении числа точек все коэффициенты вычисляются заново. Пример 2. Рассмотрим предыдущую задачу примера 1. Количество экспериментальных точек m= 3. Порядок интерполяционного полинома Лагранжа n =2. Формула (8) для n =2 будет выглядеть следующим образом:
или, подставив табличные значения, получим:
Оценка погрешности интерполяционного полинома Лагранжа
где Mn +1=max½ f(n)(x) ½ на [ a, b ].
|
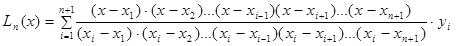(7)
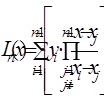. (8)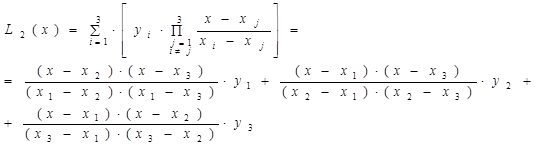
.
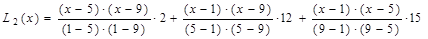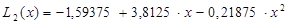, т. е. a 0 = -1, 59375, a 1 = 3, 8125, a 2 = -0, 21875. При x =3 получим L 2 (x) = 7, 875.
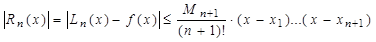, (9)
