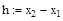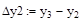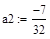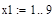Интерполирование степенными многочленами с использованием второй интерполяционной формулы Ньютона

Запрограммируем в Mathcad решение примера 4. Программировать будем также с использованием имен переменных, чтобы программа получилась универсальной.

1. Задаем системной переменной значение 1.

2. Задаем начальные значения экспериментальных массивов согласно табл. 3.

3. Строим график экспериментальных значений (рис. 26).

Рис. 26. График экспериментальных значений

4. Так как имеем три экспериментальных точки, в качестве интерполирующей зависимости выберем степенной многочлен 2-го порядка

.

Формула (11) для n =2 будет выглядеть следующим образом:

,

Dу ₂ = у ₃ – у ₂,

D ² у ₁ =D у ₂ – D у ₁ = у ₃ – 2 у ₂ + у ₁, h= 4.

Запрограммируем эти формулы в Mathcad, используя промежуточные переменные. Следует учесть при наборе следующие особенности:

1) индексы элементов экспериментальных массивов x и y набираются через клавишу; или с помощью кнопки Subscript (Нижний индекс) на панели Matrix (Матрицы);

2) имена переменных, обозначающих конечные разности, набираются в одну строку, без индексов.

Задаем функцию yr(xk) для получения расчетных значений. Имя функции отличается от y(x), чтобы не испортить заданные в начале программы значения экспериментальных массивов x и y.

Как видно, в расчетах не использовалось значение x₁, поэтому точность интерполирования выше в конце таблицы.

5. Для того чтобы получить значения коэффициентов a0, a1 и a2, воспользуемся функцией parfrac. Для этого нажмем кнопку Convert to Partial Fractions Keywords (Преобразование в частичных долях) на панели Symbolic (Символы).

Присваиваем переменным a0, a1 и a2 значения согласно полученному выражению

и высвечиваем полученные значения коэффициентов

Использование пункта 5 в программе снижает её универсальность, т. к. при изменении исходных данных эти преобразования нужно будет провести вручную.

6. Используя найденные коэффициенты, задаем функцию yr(xk) для получения расчетных значений.

7. Задаем значение контрольной точки аргумента, в которой надо найти значение искомой функции:

8. Высвечиваем расчетное значение функции в контрольной точке (как и ожидалось, оно находится между второй и третьей экспериментальными токами – 12 и 15):

9. Добавляем к построенному ранее графику экспериментальных значений расчетную кривую yr(x1). Для этого сначала вводим ранжированную переменную x1, которая позволит получить не три, а девять расчетных значений и построить более гладкий график функции, отраженный с помощью пунктирной линии (рис. 27). Значение контрольной точки отражаем на графике с помощью крестика.

Рис. 27. Графики, полученные при интерполировании с помощью

второй интерполяционной формулы Ньютона
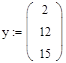
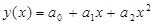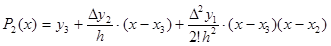