Метод неопределенных коэффициентов.
Методзаключается в том, что если в уравнение (5) подставить табличные значения
относительно коэффициентов a0, a1, ¼, an. Следует помнить, что m=n+1, где m – количество экспериментальных точек в таблице, n – количество определяемых коэффициентов. Система (6) имеет единственное решение, поскольку определитель матрицы коэффициентов (определитель Вандермонда) отличен от «0». Для решения системы линейных уравнений (6) чаще всего используют методы Крамера, Гаусса, обращения матриц (см. пункт 6.2, стр. 92) и др. Пример 1.Задание: интерполировать табличную зависимость, представленную в табл. 3. Найти значение y в контрольной точке x = 3.
Пользуясь полученной формулой, составим систему линейных уравнений:
или, подставив табличные значения, получим:
Решив полученную систему уравнений одним из методов решения систем линейных уравнений (см. пункт 6.2, стр. 92), получим значения неизвестных коэффициентов a0= – 1, 59375, a1= 3, 8125, a2= – 0, 21875. Тогда интерполяционная зависимость будет выглядеть:
При x =3 f2(x) =7, 875. Другим способом определения коэффициентов уравнения (5), позволяющим избежать решение системы уравнений (6) является построение интерполяционных многочленов, обеспечивающих равенство расчетных и экспериментальных значений функций в заданных узлах интерполирования, то есть точках (хi, yi).
|

 , то определение коэффициентов сводится к решению системы m линейных уравнений:
, то определение коэффициентов сводится к решению системы m линейных уравнений: (6)
(6) Решение. Количество экспериментальных точек m= 3. Следовательно, порядок интерполяционного многочлена n =2. Для n =2 формула (3) будет выглядеть:
Решение. Количество экспериментальных точек m= 3. Следовательно, порядок интерполяционного многочлена n =2. Для n =2 формула (3) будет выглядеть: .
.

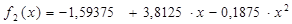 .
.


