Интерполяционные формулы Ньютона для равностоящих узлов
Интерполяционные многочлены Ньютона можно построить только при равноотстоящем расположении узлов интерполирования (точки должны быть равноотстоящие). Первая интерполяционная формула Ньютона. Пусть функция y=f(x) задана своими значениями в n+1 узлах интерполирования, т. е. y 1 = f(x 1 ); y2 = f(x 2 ); … f(xn+ 1 ); …, f(xn+ 1 ) = yn+ 1 h = xi+ 1 -xi = const, n+ 1 =m. Требуется найти многочлен Pn(x) такой, чтобы Pn(x 1 ) = f(x 1 ), Pn(x 2 ) = f(x 2 ), ¼, Pn(xn+ 1 ) = f(xn+ 1 ). Первая интерполяционная формула Ньютона имеет вид:
В этой формуле Dnу 1 означает конечную разность n -го порядка в точке у1. Понятие конечной разности связано с понятием производной. По определению производная
В нашем случае Dх = xi+ 1 – xi= h, как правило, не является бесконечно малой величиной. Приращение функции или конечная разность первого порядка в точке у1 записывается так: Dу 1 = у 2 – у 1, конечная разность второго порядка в точке у1 D 2 у1 =D у2 – D у1 =(у3 – у2)–(у2 – у1) = у3 – 2у2 + у 1 ¼ конечная разность третьего порядка в точке у1 D 3 у1=D 2 у 2 – D 2 у 1 =(Dу 3 –Dу 2 )–(Dу 2 – Dу 1 ) =Dу 3 – 2Dу 2 +D у 1 = =(у 4 –у 3 )–2(у 3 – у 2 )+ (у 2 – у 1 ) Dnу 1 = D(Dn-1y 1 ). Понятие конечной разности используется также при численном решении дифференциальных уравнений. Первая интерполяционная формула Ньютона не использует последний узел интерполирования, а значит, точность интерполирования в начале таблицы будет выше, чем в конце. Пример 3.Рассмотрим ту же задачу примера 1. Количество экспериментальных точек m= 3. Порядок 1-й интерполяционной формулы Ньютона n =2. Формула (10) для n =2 будет выглядеть следующим образом:
Dу 1 = у 2 – у 1, D2 у 1 =D у 2 – D у 1 = у 3 – 2 у 2 + у 1, h= 4 или, подставив табличные значения, получим:
a 0 = – 1, 59375, a 1 = 3, 8125, a 2 = – 0, 21875, при x =3 P 2 (x) = 7, 875. Вторая интерполяционная формула Ньютона Формула имеет вид:
Вторая формула Ньютона используется для интерполирования в конце таблицы, т. к. не рассматривает первый узел интерполирования (х1, у1). Пример 4.Рассмотрим ту же задачу примера 1. Количество экспериментальных точек m= 3. Порядок 2-й интерполяционной формулы Ньютона n =2. Формула (11) для n =2 будет выглядеть следующим образом:
Dу2 = у3 – у2, D2 у 1 =D у 2 – D у 1 = у 3 – 2у 2 + у 1, h=4.
a 0 = – 1, 59375, a 1 = 3, 8125, a 2 = – 0, 21875. При x =3 получаем P 2 (x) = 7, 875. Существуют и другие интерполяционные полиномы. Все интерполяционные полиномы предназначены для получения аналитического приближенного описания реального процесса по его n +1 экспериментальным точкам.
|

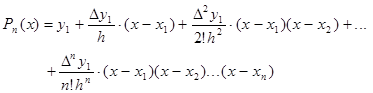 . (10)
. (10) .
. ,
, .
. .
. (11)
(11)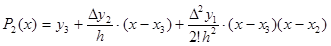 ,
, .
. .
.


