Метод выбранных точек
Из табл. 6 произвольно выбирается k точек (по числу неизвестных коэффициентов). Параметры a1 a2 ¼, ak зависимости (12) находятся, исходя из следующего условия: в выбранных точках экспериментальные рассчитанные по зависимости f(x) значения должны совпадать. Например, для квадратичной зависимости (полинома 2-го порядка)
с целью определения параметров a0 a1, a2 необходимо выбрать любые три точки (допустим, первые три). Затем, подставив табличные значения в (13), получить систему линейных алгебраических уравнений:
Решение полученной системы уравнений (14) относительно a0 a1, a2 позволяет найти параметры аппроксимирующей зависимости. Решить систему можно точным методом (Крамера, Гаусса, обращения матриц).
Линеаризация аппроксимирующей зависимости Допустим, известна структура функции, описывающей табличные данные, и она имеет следующий вид:
где z, u – известные константы. Для определения коэффициентов a0, a1, a2 необходимо выбрать три экспериментальные точки, а затем составить систему уравнений. Однако полученная система уравнений будет нелинейна относительно искомых коэффициентов и её решение сопряжено с рядом вычислительных трудностей. Чтобы избежать возникших трудностей, необходимо привести зависимость (15) к линейному виду относительно искомых коэффициентов. Для этого нужно её прологарифмировать.
и обозначить
тогда получим
Зависимость (16) линейна относительно А0, a1, a2. Её следует использовать для нахождения коэффициентов. Необходимо составить систему линейных алгебраических уравнений, решить её относительно А0, a1, a2, а затем рассчитать коэффициент а0:
|

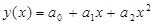 (13)
(13) . (14)
. (14)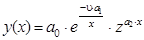 , (15)
, (15) ,
,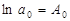 ,
, 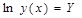
 . (16)
. (16)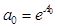 .
.


