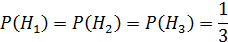Теорема гипотез и Байесовские подходы

Теорема гипотез дает возможность пересматривать принятое первоначально решение о вероятностях появления интересующих нас событий в зависимости от поступившей дополнительно информации. Байесовские методы позволяют включать ранее известные знания, убеждения и информацию, помимо тех, что содержатся в наблюдаемых данных, в процесс вывода. Сюда могут включаться данные из предыдущих исследований, известные характеристики используемой модели, и другие объективные или субъективные источники данных.

Формула Байеса – одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность того, что произошло какое-либо событие (гипотеза) при наличии лишь косвенных тому подтверждений (данных), которые могут быть неточны.

Вероятности, характеризующие суждение человека о состояниях внешнего мира и будущих событиях (иначе говоря, первоначальные вероятности гипотез) до получения дополнительной информации, называются априорными.

Вероятности, пересмотренные после получения дополнительной информации, называются апостериорными.

Априорность и апостериорность относятся к конкретной вероятности и являются понятиями относительными. Апостериорные вероятности по отношению к предшествующему наблюдению могут выступать в роли априорных по отношению к последующему наблюдению.

Формула Байеса записывается следующим образом:

где P (A) — априорная вероятность гипотезы А, — вероятность гипотезы A при наступлении события B (апостериорная вероятность), — вероятность наступления события B при истинности гипотезы A, P (B) — вероятность наступления события B.

Отношение правдоподобия – это отношение двух вероятностей получения определенного результата испытания. Оно количественно отражает влияние результата испытания на априорную вероятность:

Апостериорная вероятность = априорная вероятность x отношение правдоподобия

Современные психологи считают оптимальной моделью формирования врачом диагноза именно формулы Байеса (основную и ее модификации). Предварительный диагноз является гипотезой, сформулированной на основе априорной вероятности. Применение дополнительных методов обследования, дающих возможность получить дополнительную информацию, позволяет установить окончательный клинический диагноз с позиции апостериорной вероятности.

Многочисленные исследования, посвященные изучению процесса формирования диагноза, позволяют утверждать, что врачи могут не производить коррекцию первоначальной оценки вероятности, как правило, недооценивая последующую информацию.

Последнее качество, свойственное большинству людей, принято называть познавательным консерватизмом.

Необходимо всегда помнить, что на основе неточной или ошибочной информации нельзя получить точное и правильное решение. Именно поэтому математические методы применяются лишь в тех областях науки и практики, в которых накоплен достаточный опыт и имеется необходимый объем объективной информации.

Пример решения задачи с использованием теории вероятности

Рассмотрим простой и наглядный пример для схемы случаев. Именно для этой схемы можно точно рассчитать вероятность события, чем и объясняется столь частое к ней обращение.

Пусть имеются 3 внешне одинаковые урны, содержащие черные и белые шары. В первой урне находятся 2 белых и 1 черный шар, во второй — 3 белых и 1 черный, в третьей — 2 белых и 2 черных. Рассмотрим событие А, заключающееся в выборе белого шара из наугад выбранной урны.

В этом примере гипотезы H1, Н2, и Н3 заключаются в выборе первой, второй и третьей урны, соответственно. Поскольку все урны одинаковы, гипотезы равновозможны, отсюда вероятности выбора любой из урн одинаковы и равны:

Условные вероятности события А при каждой из гипотез определяются отношением числа белых шаров к общему числу шаров в каждой урне

Вероятность события А при наугад выбранной урне определится по формуле полной вероятности: