Пример схемы испытаний Бернулли на конкретном примере
В травматологическом отделении имеется 3 аппарата для осуществления искусственного дыхания при шоке. Больных в состоянии шока доставляют в больницу в среднем 2 раза в течение некоторого периода времени t. Вероятность отказа каждого аппарата в течение этого периода времени составляет P = 0, 1. Требуется найти вероятность наступления события А, которое заключается в том, что в течение периода времени t из трех имеющихся аппаратов два будут исправны. Обозначим через U1 U2 и U3 события, состоящие в исправности первого, второго и третьего аппарата; через P(U1) = P(U2) = P(U3) = 1 – P = 0, 9 Р( Интересующее нас событие может осуществиться тремя способами: — исправны первый и второй аппараты, неисправен — третий (событие B1); — исправны первый и третий аппараты, неисправен — второй (событие В2); — исправны второй и третий аппараты, неисправен — первый (событие В3). Эти три события являются несовместными, а элементарные события, их составляющие, — независимыми. В этой задаче мы имеем дело со схемой испытаний Бернулли. Рассматриваемые события независимы (вероятность отказа каждого из аппаратов не зависит от того, что произошло с другими двумя). Условия испытаний (функционирование аппаратов в течение времени t) остаются неизменными, так как остаются неизменными вероятности отказа каждого из них. В испытании возможны только 2 исхода: отказ или безотказная работа на протяжении времени t. Итак, нам нужно определить вероятность появления какого-либо из трех сложных несовместимых событий, каждое из которых заключается в совместном появлении трех элементарных независимых событий. Искомая вероятность может быть определена по теоремам сложения и умножения вероятностей: Р(В1) = P(U1) х P(U2) х P( Р(В2) = P(U1) х P( Р(В3) = P( Р(А) = Р(В1) + Р(В2) + Р(В3) = Р (1-Р)2 + Р (1-Р)2 + Р (1-Р)2 = 3Р (1-Р)2 Обозначим q=1-Р, тогда получим Р(А) = 3Рq2 Коэффициент «3» представляет собой число способов, которыми можно получить интересующее нас событие. Учитывая, что Р=0, 1 а q=0, 9, получим значение искомой вероятности: Р(А) = 3 х 0, 1 х 0, 92 = 0, 243
1. Вопросы по теме занятия:
1. Понятия вероятности, эксперимента, события, выборочного пространства (полной группы событий) в теории вероятности. 2. Достоверное и невозможное события. 3. Совместные и несовместные события. Понятие противоположных событий. 4. Понятия и примеры зависимых и независимых событий. 5. Равновозможные события. Понятие схемы случаев. 6. Классическая, эмпирическая и субъективная вероятности. Примеры, методы расчета. 7. Закон больших чисел. 8. Понятия суммы и произведения событий. Случаи их использования. 9. Основные теоремы теории вероятности. 10. Понятия априорной и апостериорной вероятностей. 11. Формула Байеса. 12. Схема испытаний Бернулли.
2. Тестовые задания по теме с эталонами ответов:
1. МАТЕМАТИЧЕСКАЯ НАУКА, УСТАНАВЛИВАЮЩАЯ ЗАКОНОМЕРНОСТИ СЛУЧАЙНЫХ ЯВЛЕНИЙ ЭТО 1) медицинская статистика 2) теория вероятностей 3) медицинская демография 4) высшая математика
2. ВОЗМОЖНОСТЬ РЕАЛИЗАЦИИ КАКОГО-ЛИБО СОБЫТИЯ ЭТО 1) эксперимент 2) схема случаев 3) закономерность 4) вероятность
3. ЭКСПЕРИМЕНТ ЭТО 1) процесс накопления эмпирических знаний 2) процесс измерения или наблюдения за действием с целью сбора данных 3) изучение с охватом всей генеральной совокупности единиц наблюдения 4) математическое моделирование процессов реальности
4. ПОД ИСХОДОМ В ТЕОРИИ ВЕРОЯТНОСТИ ПОНИМАЮТ 1) неопределенный результат эксперимента 2) определенный результат эксперимента 3) динамику вероятностного процесса 4) отношение числа единиц наблюдения к генеральной совокупности
5. ВЫБОРОЧНОЕ ПРОСТРАНСТВО В ТЕОРИИ ВЕРОЯТНОСТИ ЭТО 1) структура явления 2) все возможные исходы эксперимента 3) соотношение между двумя самостоятельными совокупностями 4) соотношение между двумя зависимыми совокупнос-тями
6. ФАКТ, КОТОРЫЙ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННОГО КОМП-ЛЕКСА УСЛОВИЙ, МОЖЕТ ПРОИЗОЙТИ ИЛИ НЕ ПРОИЗОЙТИ 1) частота встречаемости 2) вероятность 3) явление 4) событие
7. СОБЫТИЯ, КОТОРЫЕ ПРОИСХОДЯТ С ОДИНАКОВОЙ ЧАСТОТОЙ, И НИ ОДНО ИЗ НИХ НЕ ЯВЛЯЕТСЯ ОБЪЕКТИВНО БОЛЕЕ ВОЗМОЖНЫМ, ЧЕМ ДРУГИЕ 1) случайные 2) равновероятные 3) равнозначные 4) выборочные
8. СОБЫТИЕ, КОТОРОЕ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ ПРОИЗОЙДЕТ НЕПРЕМЕННО, СЧИТАЕТСЯ 1) нужным 2) ожидаемым 3) достоверным 4) приоритетным
9. ПРОТИВОПОЛОЖНОСТЬЮ ПО ОТНОШЕНИЮ К ДОСТОВЕРНОМУ СОБЫТИЮ ЯВЛЯЕТСЯ СОБЫТИЕ 1) ненужное 2) неожиданное 3) невозможное 4) неприоритетное
10. ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ СЛУЧАЙНОГО СОБЫТИЯ 1) больше нуля и меньше единицы 2) больше единицы 3) меньше нуля 4) представлена целыми числами
11. СОБЫТИЯ ОБРАЗУЮТ ПОЛНУЮ ГРУППУ СОБЫТИЙ, ЕСЛИ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ, ХОТЯ БЫ ОДНО ИЗ НИХ 1) появится непременно 2) появится в 90% экспериментов 3) появится в 95% экспериментов 4) появится в 99% экспериментов
12. ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ КАКОГО-ЛИБО СОБЫТИЯ ИЗ ПОЛНОЙ ГРУППЫ СОБЫТИЙ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ РАВНА 1) 0 2) 0, 95 3) 0, 99 4) 1
13. ЕСЛИ НИКАКИЕ ДВА СОБЫТИЯ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ НЕ МОГУТ ПОЯВИТЬСЯ ОДНОВРЕМЕННО, ТО ОНИ НАЗЫВАЮТСЯ 1) достоверными 2) несовместными 3) случайные 4) вероятные
14. ЕСЛИ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ НИ ОДНО ИЗ ОЦЕНИВАЕМЫХ СОБЫТИЙ НЕ ЯВЛЯЕТСЯ ОБЪЕКТИВНО БОЛЕЕ ВОЗМОЖНЫМ, ЧЕМ ДРУГИЕ, ТО ОНИ 1) равноправные 2) совместные 3) равновозможные 4) несовместимые
15. ВЕЛИЧИНА, КОТОРАЯ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ МОЖЕТ ПРИНИМАТЬ РАЗЛИЧНЫЕ ЗНАЧЕНИЯ, НАЗЫВАЕТСЯ 1) случайной 2) равновозможной 3) выборочной 4) суммарной
16. ЕСЛИ НАМ ИЗВЕСТНО КОЛИЧЕСТВО ВОЗМОЖНЫХ ИСХОДОВ НЕКОТОРОГО СОБЫТИЯ И ОБЩЕЕ КОЛИЧЕСТВО ИСХОДОВ В ВЫБОРОЧНОМ ПРОСТРАНСТВЕ, ТО МОЖНО РАССЧИТАТЬ 1) условную вероятность 2) классическую вероятность 3) эмпирическую вероятность 4) субъективную вероятность
17. КОГДА МЫ НЕ ОБЛАДАЕМ ДОСТАТОЧНОЙ ИНФОРМАЦИЕЙ О ПРОИСХОДЯЩЕМ И НЕ МОЖЕМ ОПРЕДЕЛИТЬ ЧИСЛО ВОЗМОЖНЫХ ИСХОДОВ ИНТЕРЕСУЮЩЕГО НАС СОБЫТИЯ, МЫ МОЖЕМ РАССЧИТАТЬ 1) условную вероятность 2) классическую вероятность 3) эмпирическую вероятность 4) субъективную вероятность
18. ОСНОВЫВАЯСЬ НА ВАШИХ ЛИЧНЫХ НАБЛЮДЕНИЯХ, ВЫ ОПЕРИРУЕТЕ 1) объективной вероятностью 2) классической вероятностью 3) эмпирической вероятностью 4) субъективной вероятностью
19. СУММОЙ ДВУХ СОБЫТИЙ А И В НАЗЫВАЕТСЯ СОБЫТИЕ 1) состоящее в последовательном появлении или события А, или события В, исключая совместное их появление 2) состоящее в появлении или события А, или события В 3) состоящее в появлении или события А, или события В, или событий А и В вместе 4) состоящее в появлении события А и события В совместно
20. ПРОИЗВЕДЕНИЕМ ДВУХ СОБЫТИЙ А И В ЯВЛЯЕТСЯ СОБЫТИЕ, ЗАКЛЮЧАЮЩЕЕСЯ В 1) совместном появлении событий А и В 2) последовательном появлении событий А и В 3) появлении или события А, или события В, или событий А и В вместе 4) появлении или события А, или события В
21. ЕСЛИ СОБЫТИЕ А НЕ ВЛИЯЕТ НА ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ СОБЫТИЯ В, И НАОБОРОТ, ТО ИХ МОЖНО СЧИТАТЬ 1) независимыми 2) разгруппированными 3) дистанционными 4) разнородными
22. ЕСЛИ СОБЫТИЕ А ВЛИЯЕТ НА ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ СОБЫТИЯ В, И НАОБОРОТ, ТО ИХ МОЖНО СЧИТАТЬ 1) однородными 2) сгруппированными 3) одномоментными 4) зависимыми
23. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ 1) вероятность суммы двух совместных событий равняется сумме вероятностей этих событий 2) вероятность последовательного появления двух совместных событий равняется сумме вероятностей этих событий 3) вероятность суммы двух несовместных событий равняется сумме вероятностей этих событий 4) вероятность непоявления двух несовместных событий равняется сумме вероятностей этих событий
24. СОГЛАСНО ЗАКОНУ БОЛЬШИХ ЧИСЕЛ, КОГДА ЭКСПЕРИМЕНТ ПРОВОДИТСЯ БОЛЬШОЕ ЧИСЛО РАЗ 1) эмпирическая вероятность стремится к классической 2) эмпирическая вероятность удаляется от классической 3) субъективная вероятность превышает классическую 4) эмпирическая вероятность не меняется по отношению к классической
25. ВЕРОЯТНОСТЬ ПРОИЗВЕДЕНИЯ ДВУХ СОБЫТИЙ А И В РАВНА ПРОИЗВЕДЕНИЮ ВЕРОЯТНОСТИ ОДНОГО ИЗ НИХ (А) НА УСЛОВНУЮ ВЕРОЯТНОСТЬ ДРУГОГО (В), ВЫЧИСЛЕННУЮ ПРИ УСЛОВИИ, ЧТО ПЕРВОЕ ИМЕЛО МЕСТО 1) теорема умножения вероятностей 2) теорема сложения вероятностей 3) теорема Байеса 4) теорема Бернулли
26. ОДНО ИЗ СЛЕДСТВИЙ ТЕОРЕМЫ УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ 1) если событие А зависит от события В, то и событие В зависит от события А 2) если событие А влияет на событие В, то и событие В влияет на событие А 3) если событие А не зависит от события В, то и событие В не зависит от события А 4) если событие А не влияет на событие В, то и событие В не влияет на событие А
27. ОДНО ИЗ СЛЕДСТВИЙ ТЕОРЕМЫ УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ 1) если событие А зависит от события В, то и событие В зависит от события А 2) вероятность произведения независимых событий равна произведению вероятностей этих событий 3) вероятность произведения независимых событий равна сумме вероятностей этих событий 4) вероятность произведения зависимых событий равна произведению вероятностей этих событий
28. ПЕРВОНАЧАЛЬНЫЕ ВЕРОЯТНОСТИ ГИПОТЕЗ ДО ПОЛУЧЕНИЯ ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ, НАЗЫВАЮТСЯ 1) априорными 2) апостериорными 3) предварительными 4) начальными
29. ВЕРОЯТНОСТИ, ПЕРЕСМОТРЕННЫЕ ПОСЛЕ ПОЛУЧЕНИЯ ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ, НАЗЫВАЮТСЯ 1) априорными 2) апостериорными 3) предварительными 4) окончательными
30. КАКАЯ ТЕОРЕМА ТЕОРИИ ВЕРОЯТНОСТИ МОЖЕТ ПРИМЕНЯТЬСЯ ПРИ ПОСТАНОВКЕ ДИАГНОЗА 1) Бернулли 2) Байеса 3) Чебышева 4) Пуассона
Эталоны ответов к тестовым заданиям:
|

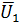 ,
, 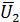 и
и  — противоположные события, состоящие в неисправности (отказе в течение времени t) первого, второго и третьего аппарата. По условию задачи вероятности этих событий равны между собой.
— противоположные события, состоящие в неисправности (отказе в течение времени t) первого, второго и третьего аппарата. По условию задачи вероятности этих событий равны между собой.


