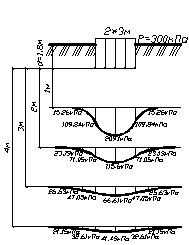
Пример расчета. Исходные данные: Р = 300 кПа, b = 2,0 м, l = 3,0 м, d = 1,8 м
Исходные данные: Р = 300 кПа, b = 2, 0 м, l = 3, 0 м, d = 1, 8 м. Необходимо определить: · напряжения в точках А, В, С, В′, C′ (рис. 33), расположенных на глубине z 1 = 1, 0 м, z 2 = 2, 0 м, z 3 = 3, 0 м, z 4 = 4, 0 м от подошвы фундамента и построить эпюры сжимающих напряжений по вертикальным и горизонтальным сечениям; · напряжения в точке М по заданным координатам xМ = 3 м, yМ = 2 м от центра фундамента, zМ = 2, 5 м.
Рис. 33. Схема определения напряжений от равномерно Последовательность расчета 1. Определим осадочное давление на подошве, принимая значение удельного веса грунта g = 16, 0 кН/м3: Р 0 = P - g d = 300 - 16, 0·1, 8 = 271, 2 кПа. 2. Найдем вертикальные напряжения на подошве фундамента в точках А, В (В ′), С (С ′): Значения коэффициента a принимаем по табл. В.1 приложения В, исходя из величин x и h. а) точка А: x = 2 z/b = 2·0/2, 0 =0 и h = l/b =3, 0/2, 0 = 1, 5. Получим a = 1.
б) точка В (В ′): загруженную площадь разбиваем на два прямоугольника I и II для каждого из которых точка В (В ′) является угловой, и напряжения находим как сумму давлений под угловыми точками двух площадей загружения. x1 = x2 = z / b = 0/1, 0 = 0 и h1 = h2 = l / b = 3, 0/1, 0 = 3. Получим a = 1.
в) точка С (С′) находится вне пределов площади загружения (рис. 33), она считается угловой для четырех фиктивных площадей загружения I, II, III и IV. x1 = x2 = z/b = 0/1, 0 = 0 и h1 = h2 = l / b = 4, 0/1, 0 = 4. Получим a = 1. x3 = x4 = z / b = 0/1, 0 = 0 и h3 = h4 = l / b = 1, 0/1, 0 =1. Получим a = 1.
3. Найдем вертикальные напряжения на глубине z = 1, 0 м. а) точка А: x = 2 z/b = 2·1, 0/2, 0 = 1, 0 и h = l/b = 3, 0/2, 0 = 1, 5. После интерполяции получим a = 0, 771.
б) точка В (В′): загруженную площадь разбиваем на два прямоугольника I и II для каждого из которых точка В (В ′) является угловой, и напряжения находим как сумму давлений под угловыми точками двух площадей загружения. x1 = x2 = z / b = 1/1, 0 = 0 и h1 = h2 =l / b = 3, 0/1, 0 = 3. Получим a = 0, 81.
в) точка С (С′) находится вне пределов площади загружения (рис. 33), она считается угловой для четырех фиктивных площадей загружения I, II, III и IV x1 = x2 = z / b = 1/1, 0 = 0 и h1 = h2 = l / b =4, 0/1, 0 = 4. Получим a = 0, 816. x3 = x4 = z / b =1/1, 0 = 0 и h3 = h 4 = l / b = 1, 0/1, 0 = 1. Получим a = 0, 703.
Аналогичным образом рассчитаем напряжения на глубинах 2, 3 и 4 м. 4. z 2 = 2 м. а) точка А: x = 2 z / b = 2·2, 0/2, 0 = 2, 0 и h = l / b = 3, 0/2, 0 = 1, 5. После интерполяции получим a = 0, 426.
б) точка В (В ′): x1 = x2 = z / b = 2/1, 0 = 2 и h1 = h2 = l/b = 3, 0/1, 0 = 3. Получим a = 0, 524.
в) точка С (С ′): x1 = x2 = z / b = 2/1, 0 = 0 и h1 = h2 = l / b = 4, 0/1, 0 = 4. Получим a = 0, 537. x3 = x4 = z/b = 2/1, 0 = 0 и h3 = h4 = l / b = 1, 0/1, 0 = 1. Получим a = 0, 366.
5. z 3 = 3 м. а) точка А: x = 2 z / b = 3·2, 0/2, 0 = 3, 0 и h = l / b = 3, 0/2, 0 = 1, 5. После интерполяции получим a = 0, 246.
б) точка В (В ′): x1 = x2 = z / b = 3/1, 0 = 3 и h1 = h2 = l / b = 3, 0/1, 0 = 3. Получим a = 0, 347.
в) точка С (С ′): x1 = x2 = z / b = 3/1, 0 = 0 и h1 = h2 = l / b = 4, 0/1, 0 = 4. Получим a = 0, 369. x3 = x4 = z / b = 3/1, 0 = 0 и h3 = h4 = l / b = 1, 0/1, 0 = 1. Получим a = 0, 18.
6. z 3 = 4 м. а) точка А: x = 2 z / b = 4·2, 0/2, 0 = 4, 0 и h = l / b = 3, 0/2, 0 = 1, 5. После интерполяции получим a = 0, 153.
б) точка В (В ′): x1 = x2 = z / b = 4/1, 0 = 3 и h1=h2 = l / b = 3, 0/1, 0 = 3. Получим a = 0, 24.
в) точка С (С ′): x1 = x2 = z / b = 4/1, 0 = 0 и h1 = h2 = l / b = 4, 0/1, 0 = 4. Получим a = 0, 264. x3 = x4 = z / b = 4/1, 0 =0 и h3 = h4 = l / b = 1, 0/1, 0 = 1. Получим a = 0, 108.
7. Строим эпюры сжимающих напряжений по вертикальным и горизонтальным сечениям (рис. 34):
а) б)
Рис. 34. Эпюры распределения сжимающих напряжений: а – по вертикальному сечению массива грунта; б – по горизонтальному сечению массива грунта
8. Определим напряжения в точке М. Точка М находится вне пределов площади загружения EFJK (рис. 35). Она считается угловой для четырех фиктивных площадей загружения I, II, III, IV (соответственно прямоугольники ELMO, JQMN, FLMN, KQMO). При этом в пределах площадей I и II направление нагрузки совпадает с направлением исходной нагрузки, а в пределах площадей III и IV направление фиктивной нагрузки является обратным направлению исходной нагрузки.
Рис. 35. Схема определения напряжений от равномерно распределенной нагрузки в точке М
x1 = z / b = 2, 5/3, 0 = 0, 833 и h1 = l / b = 4, 5/3, 0 = 1, 5. Получим a = 0, 840. x2 = z / b = 2, 5/1, 0 = 2, 5 и h2 = l / b = 1, 5/1, 0 = 1, 5. Получим a = 0, 319. x3 = z / b = 2, 5/1, 5 = 1, 667 и h3 = l / b = 3, 0/1, 5 = 2. Получим a = 0, 574. x4 = z / b = 2, 5/1, 0 = 2, 5 и h4 = l / b = 4, 5/1, 0 = 4, 5. Получим a = 0, 451.
|


 = 1·271, 2 = 271, 2 кПа;
= 1·271, 2 = 271, 2 кПа; 0 = 0, 25·(1+1)·271, 2 = 135, 6 кПа;
0 = 0, 25·(1+1)·271, 2 = 135, 6 кПа; = 0, 25·(1 + 1 – 1 - 1)·271, 2 = 0 кПа.
= 0, 25·(1 + 1 – 1 - 1)·271, 2 = 0 кПа. = 0, 771·271, 2 = 209, 6 кПа.
= 0, 771·271, 2 = 209, 6 кПа. = 0, 25· (0, 81+0, 81) ·271, 2 = 109, 84 кПа;
= 0, 25· (0, 81+0, 81) ·271, 2 = 109, 84 кПа; =0, 25· (0, 816 + 0, 816 - 0, 703 - 0, 703) ·271, 2 = 15, 26 кПа.
=0, 25· (0, 816 + 0, 816 - 0, 703 - 0, 703) ·271, 2 = 15, 26 кПа. = 0, 426·271, 2 = 115, 6 кПа.
= 0, 426·271, 2 = 115, 6 кПа. =0, 25·
=0, 25· = 0, 25·(0, 347 + 0, 347)·271, 2 = 47, 05 кПа;
= 0, 25·(0, 347 + 0, 347)·271, 2 = 47, 05 кПа;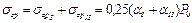 = 0, 25·(0, 24 + 0, 24)·271, 2 = 32, 61 кПа;
= 0, 25·(0, 24 + 0, 24)·271, 2 = 32, 61 кПа;