Методы оценки результатов выборочного наблюдения
Ошибки, свойственные выборочному наблюдению, называются ошибкамирепрезентативности или представительства Систематические ошибки возникают в результате нарушения принципа случайности отбора единиц совокупности для наблюдения. Например, для обследования успеваемости в университете ошибочно отбирают наиболее подготовленных студентов с положительными отметками. Случайные ошибки возникают ввиду того, что выборочная совокупность недостаточно точно воспроизводит всю совокупность из-за несплошного характера наблюдения. Средняя величина ошибки для выборочной совокупности, отобранной в случайном порядке:
где μ — средняя ошибка выборки; σ — среднее квадратическое отклонение; n — численность выборочной совокупности.
Средняя ошибка (μ) выборочных средней (х) и доли (w) для разных видов выборки
s i 2 - средняя групповая выборочная дисперсия средней: s2 i - внутригрупповая; дисперсия данной (/-и) группы в выборочной совокупности; w (1 - w) - средняя групповая выборочная дисперсия доли.
Формулы предельной ошибки позволяют решать задачи трех видов: 1. Определение пределов генеральных характеристик. 2. Определение доверительной вероятности. 3. Определение необходимого объема выборки. Предельная ошибка выборки (∆) определяется по формуле
Величины генеральной средней и доли могут быть представлены интервальной оценкой в виде определения доверительного интервала по заданному уровню доверительной вероятности Р: При значении t = 1 вероятность равна 0, 683. При значении t = 1, 96 вероятность равна 0, 950 При значении t = 2 вероятность равна 0, 954. При значении t = 3 вероятность равна 0, 997.
1. Первая оценка точности осуществляется путем сравнения известных показателей обеих совокупностей, находятся отклонения выборочной средней х от генеральной средней 2. Прямой пересчет применяется в том случае, если выборочное наблюдение проводится с целью определения объема генеральной совокупности, когда известна лишь численность генеральной совокупности, но здесь должны быть указаны доверительные интервалы: а) для средней б) для доли w - ∆ < р < w + ∆.. Формулы устанавливают границы, в которых при заданной доверительной вероятности находится неизвестная величина оцениваемого параметра: средней х или доли в генеральной совокупности. Вероятность того, что величина генеральной средней или доли выйдет за доверительные границы, равняется α = 1 - Р и называется уровнем значимости. Для вероятности Р = 0, 950 или Р = 0, 954 уровень значимости равняется соответственно 0, 050 (или 5, 0%) и 0, 046 (или 4, 6%), и превышение границ в доверительных интервалах, которое имеет такую вероятность, практически невозможно. 3. Метод поправочных коэффициентов проводится с целью уточнения результатов сплошного наблюдения. После проведения сплошного наблюдения проводится выборочное наблюдение и устанавливается так называемый процент недоучета при сплошном наблюдении. Этот процент и будет тем поправочным коэффициентом, который надо распространить на всю генеральную совокупность.
|

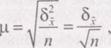
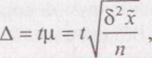
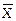 , выборочной доли w от генеральной р.
, выборочной доли w от генеральной р.


