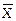Решение. Для определения границ генеральной средней необходимо рас­считать выборочную среднюю и ошибку выборочной средней

Для определения границ генеральной средней необходимо рас­считать выборочную среднюю и ошибку выборочной средней. Установим среднее количество детей в семье в выборочной со­вокупности и дисперсию выборки:

 

Количес­тво детей в семье, х	Количест во семей, /	х*/	х -	(х – )2	(x- )2 f
			-1, 46	2, 13	21, 30
			-0, 46	0, 21	4, 20
			+0, 54	0, 29	2, 90
			+ 1, 54	2, 37	9, 48
			+2, 54	6, 45	12, 90
			+3.54	12, 53	25, 06
Всего			х	х	75, 84

 

Выборочная средняя: 70/48 = 1, 46 детей

Выборочная дисперсия: σ ²= ∑ (х - )²f / ∑ f = 75, 84/48 ≈ 1, 58

Средняя квадратическая ошибка выборки относительно сред­ней при бесповторном отборе равняется:

μ = √ σ ²/n (1 - n/N) = √ 1, 58/48 (1-48/2400) = 0, 18

Заданной вероятности Р - 0, 954 отвечает коэффициент дове­рия t = 2, 0. Тогда предельная ошибка выборки равняется: ∆ = tμ = 2, 0 х 0, 18 = 0, 36 детей. Доверительный интервал для генеральной средней:

 

1, 46 - 0, 36 ≤ _р ≤, 1, 46 + 0, 36

Тогда с вероятностью 0, 954 (или 95, 4%) можно утверждать, что среднее количество детей в семье района приблизительно ле­жит в пределах 1 ≤ ≤ 2

Пример 2. Определение ошибки выборочной доли при случай­ном бесповторном и механическом отборе.

В районе города проживает 600 тыс. жителей. По материалам учета населения обследованы 60 тыс. жителей методом случай­ного бесповторного отбора. В результате обследования выбороч­ной совокупности выявлено, что в районе города 20% жителей по возрасту более 60 лет. С вероятностью 0, 683 определите грани­цы, в которых находится часть жителей в возрасте старше 60 лет. Сделайте вывод.

Решение

Генеральная доля равняется р = w ± в.. Для определения гра­ниц генеральной доли необходимо рассчитать доли выборки и предельную ошибку доли. Выборочная доля жителей в возрасте старше 60 лет составляет 20%, то есть w=0, 2.

Средняя квадратическая ошибка выборочной доли в случае бесповторного отбора составляет:

μ _w = √ w(l-w)(l-n/N)/n = √ (0, 2 х 0, 8(1-60/600))/60 = 0, 052

Вероятности 0, 683 отвечает коэффициент доверия t = 1, 0 и пре­дельная ошибка выборки равняется: ∆ = tμ =1, 0х0, 052 = 0, 052.

Доверительной интервал для генеральной доли составляет:

0, 20 -0, 052 < р< 0, 20 + 0, 052.

То есть, верхняя граница генеральной доли равняется р_в =0, 252, или 25, 2%; нижняя граница — р_н = 0, 148, или 14, 8%.

С вероятностью 0, 683 можно утверждать, что доля жителей района города в возрасте старше 60 лет находится в пределах 1 4, 8% < р< 25, 2%.

Пример 3. В области зарегистрировано 6000 малых предприятий. Определим, сколько из них нужно отобрать в порядке механического отбора для определения средней численности занятых с ошибкой ±2 чел. (Р=0, 997). По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение численности занятых составляет 9 чел.

Решение

n = 3² 9² 6000 / 3² 9² 2² 6000 = 176, 9 ~ 177

с учетом полученного необходимого объема выборки (177 предприятий) определим интервал отбора: 6000: 177 = 33, 9. Определенный таким образом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема. Следовательно, в нашем примере из общего регистра малых предприятий необходимо отбирать каждое 33 предприятие. При этом процент отбора составит 3, 03%

 

ОСНОВНЫЕ ОПРЕДЕЛЕЛЕНИЯ

 

Бесповторный отбор – процесс формирования выборочной совокупности, при котором попавшая в выборку единица в дальнейшей процедуре отбора не участвуют.

Выборочная доля – доля единиц в выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака.

Выборочная совокупность - совокупность отобранных для обсле­дования единиц.

Выборочная средняя - среднее значение изучаемого признака по

выборочной совокупности.

Выборочное наблюдение - несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистичес­кой совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уров­нем вероятности распространяются на всю исходную совокупность.

Генеральная доля - доля единиц в генеральной совокупности, обла­дающих определенным вариантом или вариантами изучаемого признака.

Генеральная совокупность - исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная.

Генеральная средняя — среднее значение изучаемого признака по

генеральной совокупности.

Метод отбора - алгоритм извлечения единиц или групп единиц из генеральной совокупности, реализующий принцип случайности отбора и лежащий в основе того или иного способа формирования выборочной совокупности (вида выборки).

Объем выборочной совокупности - планируемое или фактическое число единиц генеральной совокупности, отбираемых для регистрации

наблюдаемых признаков.

Ошибка репрезентативности - расхождение между статистически­ми характеристиками выборочной и генеральной совокупностей, обус­ловленное нарушением принципов формирования выборки или случай­ными факторами.

Повторный отбор — процесс формирования выборочной совокупно­сти, при котором попавшая в выборку единица продолжает участвовать в дальнейшей процедуре отбора и может быть отобрана в выборочную со­вокупность повторно

Вопросы для самоконтроля

1. Какое наблюдение называют выборочным и где его используют?

2. Что означает репрезентативность выборки?

3. Преимущества безповторной выборки перед повторной.

4. Что означает понятия генеральной и выборочной совокупности:

5. Как определяется предельная ошибка выборки?

6. Чем случайная ошибка репрезентативности отличается от систематической?

7. Структура формул для расчета средней ошибки и численности районов.