Статическая и дифференциальная индуктивности катушки с ферромагнитным сердечником
Пусть имеем катушку с ферромагнитным сердечником, представленную на рис. 4.
и на основании закона полного тока
Из соотношений (2) и (3) вытекает, что функция Статическая индуктивность катушки с ферромагнитным сердечником
дифференциальная индуктивность
Если магнитную проводимость сердечника на рис. 4 обозначить через
Используя соотношение (4), покажем влияние воздушного зазора на индуктивность катушки. Пусть катушка на рис. 4 имеет воздушный зазор
откуда
При
Таким образом, воздушный зазор линеаризует катушку с ферромагнитным сердечником. Зазор, для которого выполняется неравенство
Литература
Контрольные вопросы и задачи
| |||||||
| Лекция N 34. Нелинейные цепи переменного тока в стационарных режимах. |
Особенности нелинейных цепей при переменных токах
Наиболее существенная особенность расчета нелинейных цепей при переменных токах заключается в необходимости учета в общем случае динамических свойств нелинейных элементов, т.е. их анализ следует осуществлять на основе динамических вольт-амперных, вебер-амперных, и кулон-вольтных характеристик.
Если нелинейный элемент является безынерционным, то его характеристики в динамических и статических режимах совпадают, что существенно упрощает расчет. Однако на практике идеально безынерционных элементов не существует. Отнесение нелинейного элемента к классу безынерционных определяется скоростью изменения входных воздействий: если период Т переменного воздействия достаточно мал по сравнению с постоянной времени  , характеризующей динамические свойства нелинейного элемента, последний рассматривается как безынерционный; если это не выполняется, то необходимо учитывать инерционные свойства нелинейного элемента. , характеризующей динамические свойства нелинейного элемента, последний рассматривается как безынерционный; если это не выполняется, то необходимо учитывать инерционные свойства нелинейного элемента.
 В качестве примера можно рассмотреть цепь на рис.1 с нелинейным резистором (термистором), имеющим вольт-амперную характеристику (ВАХ), представленную на рис. 2, и характеризующимся постоянной времени нагрева В качестве примера можно рассмотреть цепь на рис.1 с нелинейным резистором (термистором), имеющим вольт-амперную характеристику (ВАХ), представленную на рис. 2, и характеризующимся постоянной времени нагрева  .
Если .
Если  , то изображающая точка , то изображающая точка  перемещается по прямой 1 и нелинейный резистор характеризуется сопротивлением перемещается по прямой 1 и нелинейный резистор характеризуется сопротивлением 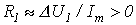 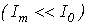 . При . При  изображающая точка перемещается по кривой 2, и свойства нелинейного резистора определяются сопротивлением изображающая точка перемещается по кривой 2, и свойства нелинейного резистора определяются сопротивлением  . Когда постоянная времени нагрева t НР одного порядка с Т, соотношения между переменными составляюшими напряжения и тока являются более сложными, определяющими сдвиг по фазе между ними.
Другой важной особенностью нелинейных элементов в цепи переменного тока является вызываемое ими появление высших гармоник даже при наличии в цепи только источников синусоидального напряжения и (или) тока. На этом принципе строится, например, ряд умножителей частоты, а также преобразователей формы тока или напряжения.
Основные типы характеристик нелинейных элементов в цепях переменного тока
Использование динамических характеристик нелинейных элементов позволяет осуществлять расчет нелинейных цепей для мгновенных значений переменных, т.е. проводить принципиально ее наиболее точный и полный анализ. Однако в целом ряде случаев такой расчет может оказаться достаточно трудоемким или избыточным по своей глубине. Поэтому в зависимости от цели решаемой задачи, а также от требований к точности получаемых результатов, помимо динамической характеристики, могут использоваться нелинейные характеристики по первым гармоникам и для действующих значений (см. табл. 1).
Таблица 1. Определение основных типов характеристик нелинейных элементов . Когда постоянная времени нагрева t НР одного порядка с Т, соотношения между переменными составляюшими напряжения и тока являются более сложными, определяющими сдвиг по фазе между ними.
Другой важной особенностью нелинейных элементов в цепи переменного тока является вызываемое ими появление высших гармоник даже при наличии в цепи только источников синусоидального напряжения и (или) тока. На этом принципе строится, например, ряд умножителей частоты, а также преобразователей формы тока или напряжения.
Основные типы характеристик нелинейных элементов в цепях переменного тока
Использование динамических характеристик нелинейных элементов позволяет осуществлять расчет нелинейных цепей для мгновенных значений переменных, т.е. проводить принципиально ее наиболее точный и полный анализ. Однако в целом ряде случаев такой расчет может оказаться достаточно трудоемким или избыточным по своей глубине. Поэтому в зависимости от цели решаемой задачи, а также от требований к точности получаемых результатов, помимо динамической характеристики, могут использоваться нелинейные характеристики по первым гармоникам и для действующих значений (см. табл. 1).
Таблица 1. Определение основных типов характеристик нелинейных элементов
|

 В соответствии с определением потокосцепления
В соответствии с определением потокосцепления ,
,
 , откуда
, откуда .
.
 качественно имеет такой же вид, что и
качественно имеет такой же вид, что и  . Таким образом, зависимости относительной магнитной проницаемости
. Таким образом, зависимости относительной магнитной проницаемости 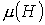 и индуктивности
и индуктивности  также подобны, т.е. представленные в предыдущей лекции на рис. 2 кривые
также подобны, т.е. представленные в предыдущей лекции на рис. 2 кривые  и
и  качественно аналогичны кривым
качественно аналогичны кривым 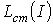 и
и  .
. ;
; .
. , то
, то  и
и  , откуда
, откуда
 . Тогда полное магнитное сопротивление контура
. Тогда полное магнитное сопротивление контура ,
, .
. , следовательно
, следовательно .
. , называется большим зазором.
, называется большим зазором. и
и  . Составить алгоритм расчета длины воздушного зазора
. Составить алгоритм расчета длины воздушного зазора  и дифференциальной
и дифференциальной  индуктивностей.
индуктивностей. 



