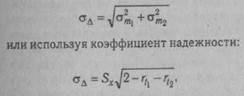Распределение ошибки измерений общего показателя теста Векслера

Колебания результатов измерений в определенном интервале значений могут быть связаны с систематическими и слу­чайными факторами. К причинам систе­матических ошибок можно отнести какое-либо отклонение от стандартного прове­дения теста, неточность в процедуре обра­ботки эмпирической информации (напр., технические ошибки в «ключе»), примене­ние методики вне пределов ее валидности по возрастному критерию. В этих случа­ях результаты измерений отличаются от истинных на более или менее постоянную величину. Случайные ошибки возникают по самым разнообразным объективным и субъективным причинам. Их величина в основном и характеризует точность метода.

При большом количестве повторных наблюдений индивидуальные оценки или средние величины образуют свой тип рас­пределения, статистические показатели которого и отражают О. и., полученные при использовании данного метода.

О. и. характеризуется величиной квад-ратической ошибки, связанной с диспер­сией распределения отдельных измере-

ний. Благодаря случайным ошибкам, за­висящим от большого количества различ­ных факторов, распределение эмпиричес­ких ошибок и средних оценок при повтор­ных наблюдениях подчиняется нормаль­ному закону. Исходя из основных свойств нормального распределения, можно счи­тать, что 68% измерений попадут в интер­вал ± 1а, около 95% — в интервал ± 2а и 99% — в пределы ± 2,58а распределе­ния оценок повторяющихся наблюдений. Таким образом, для того чтобы устано­вить, в каких пределах с заданной вероят­ностью будет находиться «истинная» оценка, необходимо определить стандарт­ное отклонение такого распределения.

В табл. 20 приведены данные 10-крат­ного обследования испытуемого с помо­щью теста общих способностей. Получен­ная в этом случае величина стандартного отклонения результата S_x = 3. Следо­вательно, с вероятностью Р = 0,05 (95% случаев) можно ожидать, что «истинное» значение величины определяемого пока­зателя попадает в интервал значений 100 ± 6 баллов, что составляет 94-106 баллов по шкале данной методики.

Показатели О. и. имеют большое зна­чение при оценке надежности методики.. Надежность теста можно выразить в виде стандартной О. и. (а_т), называемой также стандартной ошибкой показателя. При интерпретации индивидуальных показате­лей эта мера более полезна, чем коэффи­циент надежности (г,). Исходя из коэф­фициента надежности, стандартная О. и. определяется по формуле:

где S_x — стандартное "отклонение резуль­татов теста в выборке, r_t — коэффициент надежности.

Стандартная О. и. и коэффициент на­дежности — взаимосвязанные способы выражения надежности. При этом О. и. не зависит от однородности выборки.

Важным аспектом применения крите­рия О. и. в психодиагностике являются анализ и интерпретация различий между результатами теста. Представление ре­зультатов в виде интервальных вероят­ностных значений предотвращает их ошибочное толкование как отражения ре­альной динамики измеряемого свойства у испытуемого, а также необоснованность констатации различий между средними показателями в сопоставляемых выбор­ках (см. Достоверность различий, Кри­терий Х^г) при сравнении результатов не­скольких обследуемых или группы тесто­вых оценок у одного испытуемого. В пос­леднем случае при сопоставлении разных тестовых оценок, зная стандартные ошиб­ки показателей для одного и другого тес­та (или субтестов), стандартную ошибку различий (ст_д) можно определить следую­щим образом:

где S_x — стандартное отклонение, одина­ковое для двух тестов, поскольку перед сопоставлением оценок они переводятся в одну и ту же шкалу (см. Стандартиза­ция, Оценки шкальные).

Предположим, необходимо удостове­риться, существует ли у испытуемого раз­личие по оценкам вербальных и практи­ческих субтестов шкалы. Для Векслера интеллекта измерения шкалы г. вер­бальных субтестов составляет 0,96, прак­тических — 0,93, значение стандартного отклонения для той и другой шкалы — 15. Тогда

Таким образом, для установления раз­личий между оценками с доверительной вероятностью примерно 68% необходимо, чтобы разность в оценках по названным шкалам не превышала 5 баллов. При дове­рительной вероятности Р - 0,05 значение Од удваивается, приближаясь к 10 баллам.

П