Стратегии управления

 

Неотъемлемой частью ЭС, построенных на продукциях (как и любой ЭС), являются стратегии управления, которые определяют порядок применения продукционных правил. Выделяют два класса стратегий.

A) Безвозвратные стратегии. В этом случае существует критерий выбора очередного правила, после применения правила возврат к исходном состоянию (отмена применения правила) не производится никогда.

Например – игра в девять. В рассмотренном в 3.1 примере, в качестве такового выступает число фишек, находящихся «не на своем месте».

На практике, возможность применения безвозвратны стратегий ограничена, как будет показано в 3.3. коммутативными системами продукций.

B) Пробные стратегии, которые, в свою очередь, делятся на два класса – поиск с возвратом (backtracking) и поиск в пространстве состояний (или поиск на графах).

 

Поиск с возвратом.

Само название метода говорит о том, какие идеи в нем реализованы.

В начальный момент находимся в начальном состоянии ГБД. Применяем какое-нибудь правило (выбираем его по определенному критерию). В случае если приходим в тупик (не можем больше применить ни одно правило) возвращаемся на шаг назад. И так действуем до тех пор, пока не достигнем терминального состояния ГБД. В случае если произведен полный перебор вариантов, а терминальное состояние не достигнуто, значит задача неразрешима).

Главный недостаток этого метода то, что возможно зацикливание. На практике эта проблема решается путем введения ограничения на глубину поиска, что, однако, в некоторых случаях может привести к ненахождению существующего решения.

 

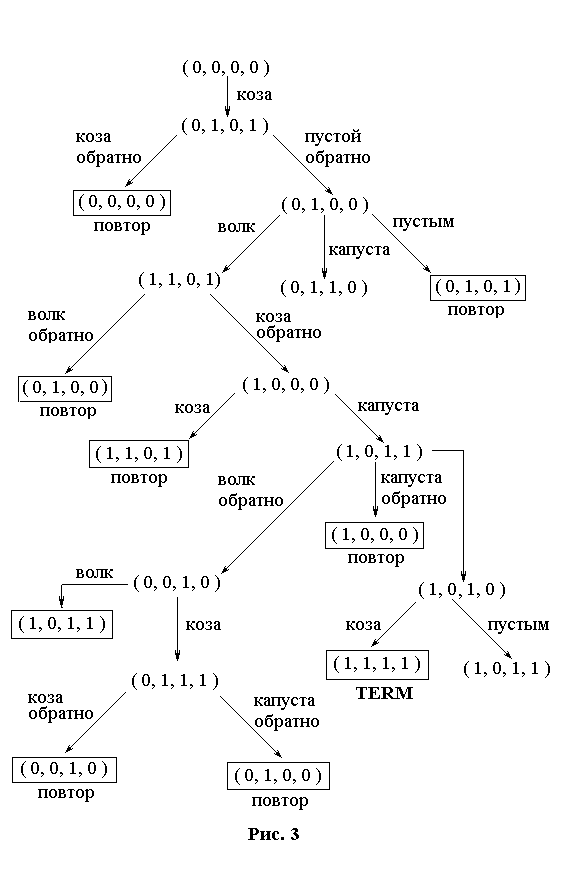
Поиск в пространстве состояний.

Понятие пространства состояний и алгоритм поиска на нем рассмотрен в 2.2.5. В данном случае в качестве вершин выступают состояния БД, а в качестве дуг – продукционные правила. Под раскрытием вершины, в данном случае, понимается применение к состоянию всех возможных правил. Рассмотрим применение метода на примере.

Пример (задача о волке, козе и капусте, используется поиск в глубину).

//пример – рисунок (3)

 

Понятие о коммутативных системах продукций

 

Коммутативной называется такая система продукций, в которой решения в случае перестановки действий остаются справедливыми.

Например, система продукций для задачи о волке, козе и капусте не является коммутативной, так как в ней порядок действий имеет значение. Примером коммутативной системы продукций может служить суммирование n чисел (каждое правило отвечает за прибавление конкретного числа).

Доказаны следующие свойства коммутативных систем продукций:

A) Каждое правило, применимое к определенному состоянию ГБД, применимо ко всем состояниям, полученным из него посредством применения конечного множества правил.

B) Если цель (терминальное состояние ГБД) может быть достигнуто из состояния D, то она может быть достигнута и из всех состояний, полученных из D.

Следствием перечисленных выше свойств является гарантия достижения цели (если это в принципе возможно) с помощью безвозратных стратегий.