Одночлены и многочлены
2 2, – 3, 3 – коэффициенты одночленов (числовой множитель).
1) Складывают только подобные 2) Умножение и деление 3) Возведение в степень
1) Сложение и вычитание ® раскрытие скобок
(a + b + c) + (a – 2 b + 3 c) = a + b + c + a – 2 b + 3 c = 2 a – b + 4 c. (a + b + c) - (a – 2 b + 3 c) = a + b + c - a + 2 b - 3 c = 3 b – 2 c. - (a + b - c) = - a – b + c. + (- x + y) = - x + y.
2) Умножение одночлена на многочлен
3) Деление многочлена на одночлен (ax + ay + az): a = x + y + z
5) Формулы сокращенного умножения:
(a – b)(a + b) =
Разложение многочленов на множители 1. Вынесение общего множителя за скобки выполняется по распределительному закону:
1) 2)
2. Группировка. Для этого надо объединить в группы те члены, которые имеют общие множители, и вынести общий множитель за скобки в каждой группе:
1) ax + 2 a – 3 x – 6 = (ax + 2 a) – (3 x + 6) = a (x + 2) – 3(x + 2) = = (x + 2)(a – 3); 2) x 2 – 2 x – xy + 2 y = (x 2 – xy) + (2 y – 2 x) = x (x – y) – 2(x – y) = = (x – y) (x – 2).
3. Применение формул сокращенного умножения позволяет разложить многочлен на множители:
1) x 2 – 4 = (x – 2)(x + 2); 2) x 2 – 6 x + 9 = (x – 3)2.
Степень и её свойства 1) 4)
Примеры: 1) (– 2)2 = 4; 2) (– 2)3 = – 8; 3) 25 = 32; 4) 5)
Содержание Линии ……………………………………………………………… 1 Углы ……………………………………………………………….. 2 Натуральные числа ……………………………………………….. 3 Степень числа …………………………………………………….. 4 Числовой луч ……………………………………………………… 4 Компоненты действий ……………………………………………. 5 Числовые и буквенные выражения ……………………………… 6 Уравнение …………………………………………………………. 7 Дроби ………………………………………………………………. 8 Основное свойство дроби ………………………………………… 9 Деление и дроби …………………………………………………... 10 Нахождение дроби от числа и числа по его дроби ……………... 11 Задачи на совместную работу ……………………………………. 11 Задачи на части ……………………………………………………. 12 Задачи на уравнивание ……………………………………………. 12 Десятичные дроби ………………………………………………… 13 Округление десятичных дробей ………………………………….. 13 Действия с десятичными дробями ……………………………….. 14 Отношение двух чисел …………………………………………… 15 Проценты ………………………………………………………….. 15 Делимость натуральных чисел …………………………………... 16 Признаки делимости ……………………………………………… 16 Задачи на движение ………………………………………………. 17 Положительные и отрицательные числа ………………………... 18 Действия над положительными и отрицательными числами …. 18 Сложение (вычитание) …………………………………………… 19 Умножение и деление …………………………………………….. 21 Решение задач с помощью уравнений …………………………… 22 Числовые выражения ……………………………………………… 23 Алгебраические выражения. Выражения с переменными …….... 23 Правило приведения подобных слагаемых …………………….... 25 Правило раскрытия скобок ……………………………………….. 26 Уравнение и его корни ……………………………………………. 27 Решение линейных уравнений …………………………………… 28 Одночлены и многочлены ………………………………………… 29 Формулы сокращенного умножения ……………………………... 29 Разложение многочленов на множители ………………………… 30 Степень и её свойства ……………………………………………... 30
|

 – одночлен 12 степени; – 3
– одночлен 12 степени; – 3  – 4 степени; 3
– 4 степени; 3  – 4 степени.
– 4 степени.



 + а – 7 xy – многочлен 3 степени.
+ а – 7 xy – многочлен 3 степени. - многочлен 4 степени.
- многочлен 4 степени.


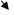

 4) Умножение многочлена на многочлен
4) Умножение многочлена на многочлен

 (a + b)(c + d) = ac + ad + bc + bd
(a + b)(c + d) = ac + ad + bc + bd





 ;
;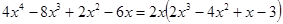 .
. , a 1 = a, a 0 = 1,
, a 1 = a, a 0 = 1, 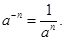
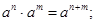 2)
2)  3)
3) 
 5)
5) 


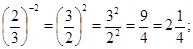 6)
6) 



