Числовые и буквенные выражения

30 × 15 + 40 = числовые выражения,

27 × 12 + 27 × 8 = их можно вычислить.

15 × 8 × 4 =

 

40 × t буквенные выражения,

30 × a + 40 их можно вычислить, если

a + b известно значение буквы.

c: 40

 

1) Найти значение выражения 2 × а + 7, если а = 7.

 

2 × а + 7 = 2 × 7 + 7 = 14 + 7 = 21.

 

2) Найти значение выражения 3 × а + 7 × b, если а = 10, b = 11.

 

3 × а + 7 × b = 3 × 10 + 7 × 11 = 30 + 77 = 107.

 

Равенства. Два выражения, соединенные знаком =.

 

верные	5 + 7 = 7 + 5	a + b = b + a
5 × 7 = 7 × 5	a × b × c = a × (b × c)
30 – 3 = 13 + 14	x + x = 2 × x
числовые равенства	буквенные равенства

 

5 + 7 = 10 – неверное равенство

а + 3 = а – неверное равенство

 

Неравенства. Два выражения, соединенные знаком < или >.

 

5 + 7 > 10

числовые

13 – 6 < 13 + 6 5 + 7 < 10

неверное неравенство

a + 7 > a

буквенные

x – 3 < x

Уравнение – равенство, содержащее неизвестное, обозначенное буквой.

 

x + 3 = 10; x = 7	Корни уравнения	Корнем уравнения называется, то значение неизвестного, при котором уравнение обращается в верное равенство. x + 3 = 10; x = 7. 7 + 3 = 10.
3 × x = 24; x = 8
x – 7 = 10; x = 17
20 – x = 15; x = 5
x: 5 = 4; x = 20
30: x = 5; x = 6

 

Решить уравнение: x + 759 = 831.

x + 759 = 831 Решить уравнение - найти его корень.

x = 831 – 759

x = 72

Проверка: 72 + 759 = 831

831 = 831

Ответ: x = 72

 

3 х = 15; х + 5 = 8; 3 х – 2 = 10; 3(х – 2) – (х + 4) = 2;

х = 15: 3; х = 8 – 5; 3 х = 10 + 2; 3 х – 6 – х – 4 = 2;

х = 5. х = 3. 3 х = 12; 3 х – х = 2 + 4 + 6;

х = 12: 3; 2 х = 12;

х = 4. х = 6.

 

Решение задач с помощью уравнений.

П – х

Б – х + 17 всего 75 кг

(на 17 кг больше)

____________________________

х + х + 17 = 75

 

1) х кг – сахара в полиэтиленовом мешке

(меньшая величина)

2) (х + 17) кг – сахара в бумажном мешке.

3) Всего сахара – 75 кг.

Составим уравнение:

х + х + 17 = 75; 2 х +17 = 75; 2 х = 75 – 17;

2 х = 58; х = 29.

х + 17 = 29 + 17 = 46. Ответ: 46 кг, 29 кг.

Дроби

1) 20 см = м; 1 230 мин. =? ч.

Дробные числа получаются при измерениях. 500 г = кг

2) Знаменатель дроби показывает на сколько равных частей разделили целое.

Числитель дроби показывает сколько таких частей взято.

 

 

 

числитель знаменатель

; ; ; - дробные числа (обыкновенные дроби).

 

3) 1 доля или несколько долей единицы называется дробью.

4)

^{| | | | | |}

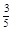
1 целое половина

треть четверть

 

 

0 правильная 1 2

| | | | | | | | | | | | | | | | |

неправильная