Положительные и отрицательные числа
– 3 0 3 противоположные: а и – а; – 20 и – (– 20) = 20; – 52 и 52.
натуральные противоположно Z = натуральные
Модуль: 1) число без знака 2) расстояние в единичных отрезках
Действия над положительными и отрицательными числами
1) модули ×; или: 2) знак
Действия с рациональными числами.
Сложение (вычитание) Любое выражение, содержащее знаки сложения и вычитания, можно рассматривать как сумму: а - b = а + (- b).
Чтобы сложить два отрицательных числа, нужно: 1) сложить их модули; 2) поставить перед полученным числом знак «-».
Вспомните!
|
Например:
|


Например: общий знак
 |


 - 3 – 5 = - 3 + - 5 = - 8 = - 8
- 3 – 5 = - 3 + - 5 = - 8 = - 8
| Задание | Решение |
| Вычислите: – 8 – 21. | – 8 – 21 = – (8 + 21) = – 29. Ответ: – 29. |
Чтобы сложить два числа с разными знаками, нужно:
1) из большего модуля слагаемых вычесть меньший;
2) поставить перед полученным числом знак того слагаемого, модуль которого больше.
Например: знак большего числа
по модулю







 3 – 5 = + 3 + (- 5) = - 2 = - 2
3 – 5 = + 3 + (- 5) = - 2 = - 2
знак большего числа
по модулю






 - 3 + 5 = - 3 + 5 = + 2 = 2
- 3 + 5 = - 3 + 5 = + 2 = 2
| Задание | Решение |
| Вычислите: 1) 12 – 18; 2) – 6,3 + 4,1. | 1) 12 – 18 = – (18 – 12) = – 6; 2) – 6,3 + 4,1 = – (6,3 – 4,1) = – 2,2. |
Действия с рациональными числами.



 - +
- +

 · · ·
· · ·


 + + 1) «объединяются»
или
- - 2) общий язык
1) «воюют»
+ и - 2) знак
«победителя»
+ + 1) «объединяются»
или
- - 2) общий язык
1) «воюют»
+ и - 2) знак
«победителя»

 - = раскрытие
скобок и +
- = раскрытие
скобок и +


 - (+) = -
- (+) = - + (-) = -
+ (-) = -

 модуль –5
модуль –5 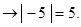



 5единиц 5единиц
модуль – расстояние
5единиц 5единиц
модуль – расстояние



