Задача 5. Через точку 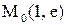 поверхности
поверхности 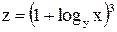 проведены плоскости, параллельные координатным плоскостям XOZ и YOZ. Определить углы, которые образуют с осями координат OX и OY касательные к получившимся сечениям, проведенные в их общей точке
проведены плоскости, параллельные координатным плоскостям XOZ и YOZ. Определить углы, которые образуют с осями координат OX и OY касательные к получившимся сечениям, проведенные в их общей точке 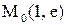 (рис. 3).
(рис. 3).
Решение. Геометрический смысл частных производных первого порядка 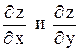 функции
функции 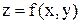 состоит в том, что частные значения этих частных производных, вычисленные в точке касания, определяют тангенсы углов наклона к соответствующим осям касательных к образовавшимся сечениям, проведенных в точке касания
состоит в том, что частные значения этих частных производных, вычисленные в точке касания, определяют тангенсы углов наклона к соответствующим осям касательных к образовавшимся сечениям, проведенных в точке касания 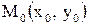 – это тангенсы углов наклона к соответствующим осям касательных в этой точке к кривым, которые образуются при пересечении поверхности
– это тангенсы углов наклона к соответствующим осям касательных в этой точке к кривым, которые образуются при пересечении поверхности 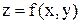 плоскостями
плоскостями 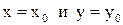 , т. е.
, т. е.
 z
M0
0 y0 y
β
x0
х
α
Рис. 3 z
M0
0 y0 y
β
x0
х
α
Рис. 3
| с осью OX:  ;
с осью OY: ;
с осью OY: 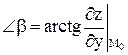 ; ;
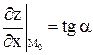 ; ; 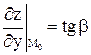 .
Для отыскания производных данной функции преобразуем ее, используя формулу: .
Для отыскания производных данной функции преобразуем ее, используя формулу:
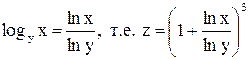 . .
|
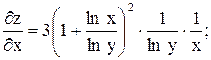
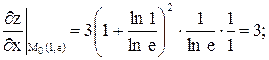
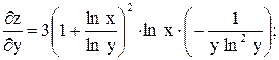

Ответ:  .
.
Задача 6. Найти частные производные второго порядка функции 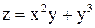 .
.
Решение. 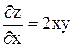 ,
, 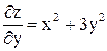 ,
,
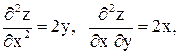
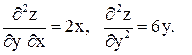
Заметим, что 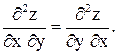
Задача 7. Найти 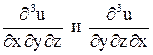 , если
, если 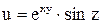 .
.
Решение. Вначале найдем  .
.
 ;
;  ;
;
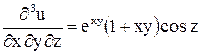 .
.
Теперь найдем 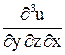 .
.
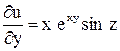 ;
;  ;
;
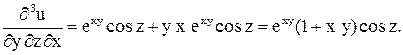
Сравнив ответы, убеждаемся в том, что частные производные смешанного типа не зависят от порядка дифференцирования.
Задача 8. Дана функция 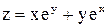 . Доказать, что эта функция удовлетворяет уравнению
. Доказать, что эта функция удовлетворяет уравнению 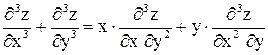 .
.

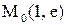 поверхности
поверхности 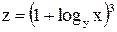 проведены плоскости, параллельные координатным плоскостям XOZ и YOZ. Определить углы, которые образуют с осями координат OX и OY касательные к получившимся сечениям, проведенные в их общей точке
проведены плоскости, параллельные координатным плоскостям XOZ и YOZ. Определить углы, которые образуют с осями координат OX и OY касательные к получившимся сечениям, проведенные в их общей точке 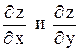 функции
функции 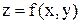 состоит в том, что частные значения этих частных производных, вычисленные в точке касания, определяют тангенсы углов наклона к соответствующим осям касательных к образовавшимся сечениям, проведенных в точке касания
состоит в том, что частные значения этих частных производных, вычисленные в точке касания, определяют тангенсы углов наклона к соответствующим осям касательных к образовавшимся сечениям, проведенных в точке касания 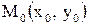 – это тангенсы углов наклона к соответствующим осям касательных в этой точке к кривым, которые образуются при пересечении поверхности
– это тангенсы углов наклона к соответствующим осям касательных в этой точке к кривым, которые образуются при пересечении поверхности 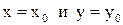 , т. е.
, т. е. z
M0
0 y0 y
β
x0
х
α
Рис. 3
z
M0
0 y0 y
β
x0
х
α
Рис. 3
 ;
с осью OY:
;
с осью OY: 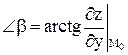 ;
;
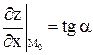 ;
; 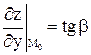 .
Для отыскания производных данной функции преобразуем ее, используя формулу:
.
Для отыскания производных данной функции преобразуем ее, используя формулу:
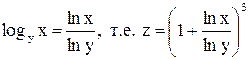 .
.
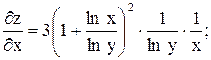
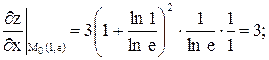
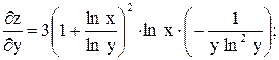

 .
.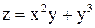 .
.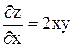 ,
, 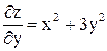 ,
,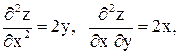
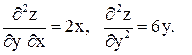
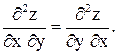
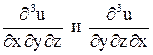 , если
, если 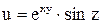 .
. .
. ;
;  ;
;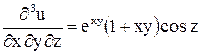 .
.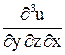 .
.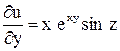 ;
;  ;
;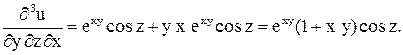
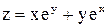 . Доказать, что эта функция удовлетворяет уравнению
. Доказать, что эта функция удовлетворяет уравнению 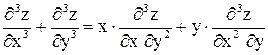 .
.


