а) Уравнения касательной в точке  к пространственной кривой
к пространственной кривой
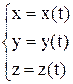 :
: 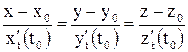 , где
, где  – направляющий
– направляющий
вектор касательной,  – точка касания.
– точка касания.
б) Уравнения касательной плоскости  и нормали
и нормали  к поверхности
к поверхности 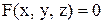 в точке
в точке  .
.
 .
.
 .
.
 n
n
z
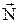
| |
| | 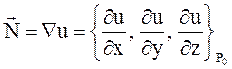 (рис. 8) (рис. 8)
| |
α
P0
0 у
x Рис. 8
Задача 23. Составить уравнение касательной прямой к пространственной линии  .
.
Решение. Уравнение касательной к пространственной кривой в общем виде таково: 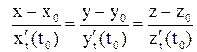 . Найдем координаты точки касания:
. Найдем координаты точки касания:


 , затем координаты направляющего вектора
, затем координаты направляющего вектора 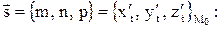
 .
.
Итак,  – касательная к пространственной кривой в данной точке.
– касательная к пространственной кривой в данной точке.
Задача 24. Составить уравнения касательной плоскости и нормали к поверхности  (гиперболический параболоид) в точке
(гиперболический параболоид) в точке  .
.
Решение. Вначале запишем уравнение данной поверхности в виде 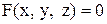 , т. е.
, т. е.  . Тогда уравнение касательной плоскости в общем виде запишется так:
. Тогда уравнение касательной плоскости в общем виде запишется так: 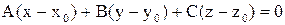 ,
,
где  ,
,  ,
, 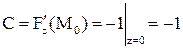 ,
,
т. е. нормаль к касательной плоскости  – точка касания, значит,
– точка касания, значит, 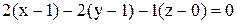 , т. е.
, т. е.  – касательная плоскость к данной поверхности в точке
– касательная плоскость к данной поверхности в точке  .
.
Уравнения нормали к этой же поверхности в точке  в общем виде запишутся так:
в общем виде запишутся так:  – направляющий вектор нормали, за него можно принять нормаль к касательной плоскости
– направляющий вектор нормали, за него можно принять нормаль к касательной плоскости 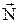 , т. е.
, т. е.  . Итак,
. Итак,  – это канонические уравнения нормали к данной поверхности в точке
– это канонические уравнения нормали к данной поверхности в точке  .
.
Задача 25. Показать, что конус  и сфера
и сфера 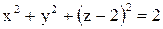 касаются друг друга в точке
касаются друг друга в точке  .
.
Решение. Чтобы решить задачу, достаточно показать, что в точке  данные конус и сфера имеют общую касательную плоскость:
данные конус и сфера имеют общую касательную плоскость:
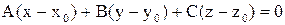 .
.
Сначала найдем касательную плоскость к конусу в точке  : уравнение конуса запишем в виде
: уравнение конуса запишем в виде  , т. е. в виде
, т. е. в виде  , откуда
, откуда
 ,
,  ,
,  .
.
Значит,  – касательная плоскость к конусу в точке
– касательная плоскость к конусу в точке  .
.
Также найдем касательную плоскость к сфере  в точке
в точке  .
.
 ,
,  ,
,  .
.
Касательная плоскость к сфере в точке  задается уравнением
задается уравнением

 , что и требовалось доказать.
, что и требовалось доказать.
Задача 26. На поверхности  найти точки, в которых касательная плоскость параллельна координатной плоскости XOZ.
найти точки, в которых касательная плоскость параллельна координатной плоскости XOZ.
Решение. Так как касательная плоскость к поверхности параллельна плоскости XOZ, то она перпендикулярна оси OY и ее нормаль 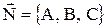 имеет координаты
имеет координаты  . С другой стороны известно, что нормаль касательной плоскости к поверхности
. С другой стороны известно, что нормаль касательной плоскости к поверхности  имеет координаты:
имеет координаты:
 .
.
Чтобы найти  , сравним А, В и С вектора
, сравним А, В и С вектора 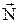 :
:  ,
,  ,
,  , т. е.
, т. е. 

 – координаты точки касания. Осталось
– координаты точки касания. Осталось
найти В. Так как точка касания принадлежит поверхности, ее координаты должны удовлетворять уравнению этой поверхности:
 , откуда
, откуда  значит
значит  . Значит, точек касания две:
. Значит, точек касания две:  и
и 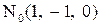 .
.

 к пространственной кривой
к пространственной кривой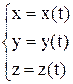 :
: 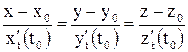 , где
, где  – направляющий
– направляющий – точка касания.
– точка касания. и нормали
и нормали  к поверхности
к поверхности 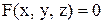 в точке
в точке  .
. .
. n
n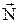
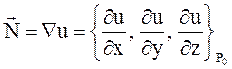 (рис. 8)
(рис. 8)
 .
.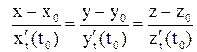 . Найдем координаты точки касания:
. Найдем координаты точки касания:

 , затем координаты направляющего вектора
, затем координаты направляющего вектора 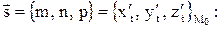
 .
. – касательная к пространственной кривой в данной точке.
– касательная к пространственной кривой в данной точке. (гиперболический параболоид) в точке
(гиперболический параболоид) в точке  .
.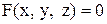 , т. е.
, т. е.  . Тогда уравнение касательной плоскости в общем виде запишется так:
. Тогда уравнение касательной плоскости в общем виде запишется так: 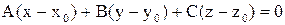 ,
, ,
,  ,
, 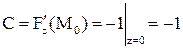 ,
, – точка касания, значит,
– точка касания, значит, 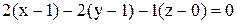 , т. е.
, т. е.  – касательная плоскость к данной поверхности в точке
– касательная плоскость к данной поверхности в точке  .
. – направляющий вектор нормали, за него можно принять нормаль к касательной плоскости
– направляющий вектор нормали, за него можно принять нормаль к касательной плоскости  . Итак,
. Итак,  – это канонические уравнения нормали к данной поверхности в точке
– это канонические уравнения нормали к данной поверхности в точке  и сфера
и сфера 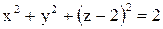 касаются друг друга в точке
касаются друг друга в точке  .
. данные конус и сфера имеют общую касательную плоскость:
данные конус и сфера имеют общую касательную плоскость: , т. е. в виде
, т. е. в виде  , откуда
, откуда ,
,  ,
,  .
. – касательная плоскость к конусу в точке
– касательная плоскость к конусу в точке  в точке
в точке  .
.
 , что и требовалось доказать.
, что и требовалось доказать. найти точки, в которых касательная плоскость параллельна координатной плоскости XOZ.
найти точки, в которых касательная плоскость параллельна координатной плоскости XOZ.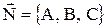 имеет координаты
имеет координаты  . С другой стороны известно, что нормаль касательной плоскости к поверхности
. С другой стороны известно, что нормаль касательной плоскости к поверхности  .
. , сравним А, В и С вектора
, сравним А, В и С вектора  ,
,  ,
,  , т. е.
, т. е. 

 – координаты точки касания. Осталось
– координаты точки касания. Осталось , откуда
, откуда  значит
значит  . Значит, точек касания две:
. Значит, точек касания две: 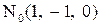 .
.


