Элементы скалярного поля
а) Производная скалярного поля
 z
M β α
0 у
x Рис. 6
Задача 19. Найти скорость изменения скалярного поля Решение. Скорость изменения скалярного поля в направлении вектора
В задаче
Подставим все найденные величины в первую формулу:
Ответ: В заданном направлении данное скалярное поле убывает со скоростью
б) Градиент скалярного поля
Очевидно,
Рис. 7 Задача 20. Найти величину градиента скалярного поля Решение.
Ответ:
Задача 21. Найти наибольшую скорость возрастания скалярного поля
Решение. Воспользуемся формулой
Ответ:
Задача 22. Функция Решение. Найдем вначале градиент u по формуле
Так как скалярный квадрат вектора равен квадрату его модуля, то
Теперь все известные величины можно подставить в уравнение:
|
по направлению вектора
(рис.6).
определяется так: 
– это скорость изменения скалярного поля 
в направлении вектора 
.
в точке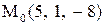 
в направлении от этой точки к точке 
.
определяют по формуле
.
, 
,
.
,
,
.
.
.
.
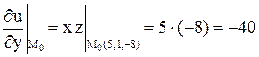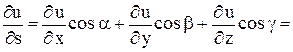
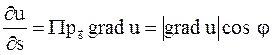(рис. 7).
в точке 
.
.
.
.
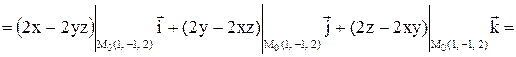
в точке 
.
,
.
.
определяет скалярное поле. Доказать, что она удовлетворяет уравнению 
.
, или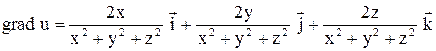 
. Из полученного равенства следует, что декартовы координаты 
.
.
, т. е. 
, что и требовалось доказать.
