Правило. Чтобы найти М – наибольшее и m – наименьшее значения функции  в замкнутой области D, находят критические точки этой функции. Если эти точки принадлежат области D, то в них следует вычислить значения
в замкнутой области D, находят критические точки этой функции. Если эти точки принадлежат области D, то в них следует вычислить значения  . Затем, используя уравнения границы L области D, нужно найти критические точки
. Затем, используя уравнения границы L области D, нужно найти критические точки  , принадлежащие L, вычислить в них значения
, принадлежащие L, вычислить в них значения  . Вычислить значения
. Вычислить значения  на концах L. Осталось из всех найденных значений данной функции
на концах L. Осталось из всех найденных значений данной функции  выбрать самое большое М и самое малое m.
выбрать самое большое М и самое малое m.
Задача 17. Найти наибольшее М и наименьшее m значения функции 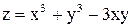 в прямоугольнике
в прямоугольнике  .
.
Решение. Найдем критические точки функции z, которые принадлежат заданной области (рис. 4).

У
B(0, 2)  C(2, 2)
C(2, 2)
Решим систему уравнений
 подставим
подставим  во второе уравнение: во второе уравнение:  , т. е. , т. е. 

| |
y=2
1 

x=2
 1 2 x
1 2 x
у=-1
A(0, -1) D(2, -1)
Рис. 4
Таким образом, решений у системы два:  . Первому решению соответствует точка
. Первому решению соответствует точка  , которая принадлежит границе области. Второму решению соответствует критическая точка
, которая принадлежит границе области. Второму решению соответствует критическая точка  , которая принадлежит области, поэтому вычислим значения функции в ней:
, которая принадлежит области, поэтому вычислим значения функции в ней: 
 .
.
Исследуем функцию z на границе области (прямоугольник ABCD), которая состоит из четырех звеньев:
1. АВ:  . Получаем критическую точку
. Получаем критическую точку  , вычислим функцию в этой точке:
, вычислим функцию в этой точке: 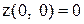 .
.
2. ВС:  . Найдем произ-водную этой функции:
. Найдем произ-водную этой функции:  , корень уравнения
, корень уравнения  , поэтому критическая точка
, поэтому критическая точка  . Вычислим значение функции в ней:
. Вычислим значение функции в ней:  .
.
 .
.
3. СD:  . Найдем
. Найдем  , а
, а  . Поэтому критическая точка
. Поэтому критическая точка  . Вычислим в ней значение функции:
. Вычислим в ней значение функции:


 .
.  .
.
4. AD:  . Найдем производную этой функции:
. Найдем производную этой функции:  , действительных корней не имеет.
, действительных корней не имеет.
5. Осталось вычислить значения функции  на концах каждого из отрезков, являющихся сторонами прямоугольника: АВ, BC, CD, AD, т. Е. в вершинах прямоугольника
на концах каждого из отрезков, являющихся сторонами прямоугольника: АВ, BC, CD, AD, т. Е. в вершинах прямоугольника  .
.

 ,
,

 ,
,
 ,
,  ,
,
 ,
, 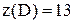 .
.
Сравнив все подчеркнутые значения функции z (только они представляют интерес), делаем вывод: наибольшее значение z достигает в вершине прямоугольника D, т. Е.  , а наименьшее – в двух точках: во внутренней точке области
, а наименьшее – в двух точках: во внутренней точке области  и в вершине
и в вершине  .
.
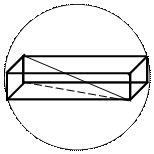
Задача 18. В шар, диаметр которого равен 2R, вписать прямоугольный параллелепипед наибольшего объема (рис. 5).
| |
| | Решение.Обозначим x, y, z – стороны параллелепипеда, тогда  . Из рис. 5 видно: . Из рис. 5 видно:  , , 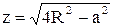 , т. е. , т. е.  ,
значит, ,
значит,  , где , где  , ,  . .
| |
2R
z a y
x
Рис. 5
 ;
;
 ,
,
или 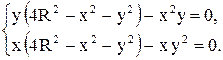
Из условия задачи  ,
,
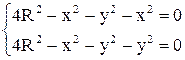 или
или 
 ,
,
откуда  , т. е. прямоугольный параллелепипед, вписанный в данный шар, будет иметь наибольший объем, если он будет кубом, ребра которого равны
, т. е. прямоугольный параллелепипед, вписанный в данный шар, будет иметь наибольший объем, если он будет кубом, ребра которого равны  .
.

 в замкнутой области D, находят критические точки этой функции. Если эти точки принадлежат области D, то в них следует вычислить значения
в замкнутой области D, находят критические точки этой функции. Если эти точки принадлежат области D, то в них следует вычислить значения 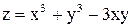 в прямоугольнике
в прямоугольнике  .
.

 C(2, 2)
C(2, 2) подставим
подставим  во второе уравнение:
во второе уравнение:  , т. е.
, т. е. 



 1 2 x
1 2 x . Первому решению соответствует точка
. Первому решению соответствует точка  , которая принадлежит границе области. Второму решению соответствует критическая точка
, которая принадлежит границе области. Второму решению соответствует критическая точка  , которая принадлежит области, поэтому вычислим значения функции в ней:
, которая принадлежит области, поэтому вычислим значения функции в ней: 
 .
. . Получаем критическую точку
. Получаем критическую точку  , вычислим функцию в этой точке:
, вычислим функцию в этой точке: 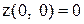 .
. . Найдем произ-водную этой функции:
. Найдем произ-водную этой функции:  , корень уравнения
, корень уравнения  , поэтому критическая точка
, поэтому критическая точка  . Вычислим значение функции в ней:
. Вычислим значение функции в ней:  .
. .
. . Найдем
. Найдем  , а
, а  . Поэтому критическая точка
. Поэтому критическая точка  . Вычислим в ней значение функции:
. Вычислим в ней значение функции:

 .
.  .
. . Найдем производную этой функции:
. Найдем производную этой функции:  , действительных корней не имеет.
, действительных корней не имеет. на концах каждого из отрезков, являющихся сторонами прямоугольника: АВ, BC, CD, AD, т. Е. в вершинах прямоугольника
на концах каждого из отрезков, являющихся сторонами прямоугольника: АВ, BC, CD, AD, т. Е. в вершинах прямоугольника  .
.
 ,
,
 ,
, ,
,  ,
, ,
, 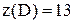 .
. , а наименьшее – в двух точках: во внутренней точке области
, а наименьшее – в двух точках: во внутренней точке области  и в вершине
и в вершине  .
. . Из рис. 5 видно:
. Из рис. 5 видно:  ,
, 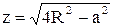 , т. е.
, т. е.  ,
значит,
,
значит,  , где
, где  ,
,  .
.

 ;
; ,
,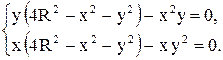
 ,
,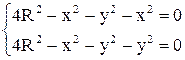 или
или 
 ,
, , т. е. прямоугольный параллелепипед, вписанный в данный шар, будет иметь наибольший объем, если он будет кубом, ребра которого равны
, т. е. прямоугольный параллелепипед, вписанный в данный шар, будет иметь наибольший объем, если он будет кубом, ребра которого равны  .
.


