Решение.
Подставим в уравнение найденные значения производных:
что и требовалось доказать.
Производная сложной функции а) Если
б) Если
в) Если
Задача 9. Дана функция ты. Найти
Решение.
Задача 10. Дана функция
Решение. Очевидно, что u – сложная функция одной независимой перемен- ной t, а x, y и z – промежуточные аргументы, т. е. существует
Задача 11. Найти
Решение.
Сравните:
Производная функции, заданной неявно а) Если
б) Если
Задача 12. Дано:
Решение. Данное уравнение задает неявно функцию z, зависящую от переменных х и у. Запишем данное уравнение в виде
Очевидно:
Приложения производных функции
Полный дифференциал функции двух переменных
|

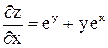






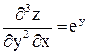 .
.
 ,
, , где
, где 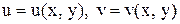 , то
, то  - сложная функция двух переменных х и у, тогда
- сложная функция двух переменных х и у, тогда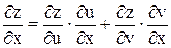 ;
;  .
.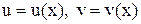 , то
, то  - сложная функция одной переменной х, тогда
- сложная функция одной переменной х, тогда - полная производная сложной функции одной независимой переменной х.
- полная производная сложной функции одной независимой переменной х.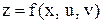 , где
, где  - сложная функция одной переменной х и
- сложная функция одной переменной х и .
. , где
, где 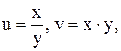 т. е.
т. е. 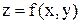 – сложная функция двух переменных х и у, где u и v - промежуточные аргумен-
– сложная функция двух переменных х и у, где u и v - промежуточные аргумен-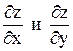 .
. ;
;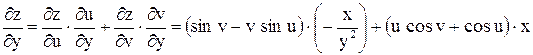 .
. . Найти
. Найти 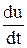 .
.
 .
. , если
, если  , где
, где  .
.
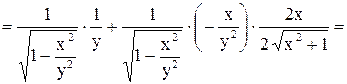
 , если
, если  , т.к.
, т.к.  .
. , то у – функция одной переменной х, заданная неявно.
, то у – функция одной переменной х, заданная неявно.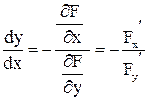 .
. , то z – функция двух независимых переменных, заданная неявно.
, то z – функция двух независимых переменных, заданная неявно. ;
;  .
. . Доказать, что
. Доказать, что  .
. . Очевидно, что
. Очевидно, что .
. ;
; .
. , что и требовалось доказать.
, что и требовалось доказать.


