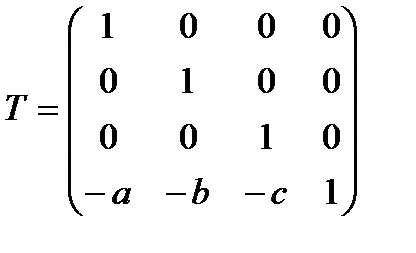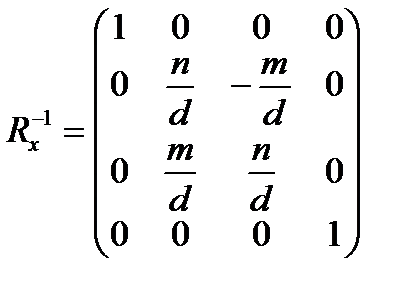Поворот вектора (точки) вокруг произвольной оси
Вы можете увидеть этот вывод в книге Е.В. Шикин А.В. Боресков. Компьютерная графика. — М:, Диалог МИФИ, 1995. Построить матрицу поворота точки на угол φ вокруг прямой L, проходящей через точку A (a,b,c) и имеющую направление (l,m,n). Направляющий вектор нормирован, т.е.
Решение состоит из 7-ми шагов: ¨ Перенос прямой L на вектор –А (–a, –b, –c) так, чтобы она проходила через начало координат. ¨ Поворот вокруг оси абсцисс на угол ψ. ¨ Поворот вокруг оси ординат на угол θ. ¨ Вращение вокруг прямой L (то есть вокруг оси Z) на заданный угол φ. ¨ Обратный поворот вокруг оси ординат на угол –θ. ¨ Обратный поворот вокруг оси абсцисс на угол – ψ. ¨ Обратный перенос прямой L на вектор А (a, b, c) Шаги 2 и 3 являются совмещением оси аппликат с прямой L с помощью двух поворотов. Решение — искомую матрицу — можно записать в виде произведения 7-ми матриц.
Рассмотрим, как получить все эти 7 матриц. На первом шаге мы получаем матрицу сдвига.
На втором шаге — матрицу вращения вокруг оси x.
На третьем шаге — матрицу вращения вокруг оси y.
На четвертом шаге — матрицу вращения вокруг прямой L на заданный угол φ.
На пятом шаге — матрицу обратного вращения вокруг оси y.
На шестом шаге — матрицу обратного вращения вокруг оси x.
Вам осталось собрать все фрагменты и получить общий вид матрицы поворота. Ниже приведен другой, геометрический (классический) подход к выводу формулы для матрицы поворота вокруг произвольной оси.
|