Немного теории
Сплайном в математике называется полином (обычно) третьей степени, который описывает кривую, проходящую через две контрольные точки.
Для того, чтобы найти четыре коэффициента полинома можно составить и решить систему из четырех уравнений. Например, два уравнения получить из условия, что контрольные точки должны лежать на кривой, а недостающие два получить, задав значения производных (то есть наклона кривых) в двух контрольных точках.
Если имеется три контрольные точки, то два полинома (сплайна) сопрягаются в промежуточной точке таким образом, чтобы в ней не было излома общей кривой. Для этого оба сплайна в контрольной точке должны иметь равные значения как функции, так и двух ее производных. Для решения задачи следует составить систему из 8 уравнений для определения 8 коэффициентов 2 полиномов. Четыре уравнения получаются из условия принадлежности контрольных точек кривым, два уравнения из условия равенства первых двух производных в точке сопряжения и последние два путем задания наклонов кривых в граничных точках. Эти условия равносильны заданию первых производных в точках. При четырех контрольных точках то есть трех полиномах, надо решать систему из 12 уравнений и т.д. На самом деле математики нашли способ решать систему уравнений, порядок которой значительно ниже. Он равен числу контрольных точек, исключая граничные, но исходная система составляется не для коэффициентов полиномов, а для значений вторых производных в контрольных точках. После решения системы искомые коэффициенты определяются по формулам, полученным из условий линейности второй производной от полинома третьей степени и равенства полиномов в точках сопряжения. Сплайны, то есть коэффициенты OpenGL пользуется сплайнами и поверхностями, описываемыми в базисе Bézier, который иногда называют базисом Bernstein. Кривой Bézier в пространстве называется траектория, вектор координат которой задан параметрически. f(t) = [ x(t), y(t), z(t) ] Параметр t изменяется в нормированном диапазоне [0,1]. Если представить, что t — это время, то при изменении его от нуля до единицы, то точка (или вектор) с координатами f(t) пройдет по траектории от начала до конца. Аналогично, поверхность Bézier — это вектор, координаты которого являются функциями двух параметров. f(t,u) = [ x(t,u), y(t,u), z(t,u) ] При каждом фиксированном u = с функция f(t, c) задает в трехмерном пространстве какую-то кривую Bézier. Далее, измененяя u в диапазоне от 0 до 1, мы получим множество кривых, которое опишет поверхность. Вектор может иметь и другое число компонентов. Для кривых на проскости или для координат текстуры можно использовать лишь две координаты. Для вектора RGBA цвета можно использовать 4 координаты. Для задания цвета в виде оттенка серого можно использовать лишь одну координату. При вычислении координат точек кривой вместо функции glVertex * используются функции glEvalCoord1 * или glEvalCoord2 *. Первая вычисляет f(t), а вторая — f(t, u). Обычно первая вызываются в цикле по параметру t и, поэтому, генерирует точки. для каждого значения параметра. Вторая вызывается внутри двойного цикла (по двум параметрам t и u).
|


 (i = 0,1,2,3) вычисляются с помощью OpenGL. Для этого используются функции из семейства glMap*. Если мы нашли коэффициенты сплайна, аппроксимирующего поведение кривой между двумя контрольными точками, то такой инструмент OpenGL как evaluator (или функция из семейства glEvalCoord*), может сгенерировать произвольное количество N промежуточных точек (
(i = 0,1,2,3) вычисляются с помощью OpenGL. Для этого используются функции из семейства glMap*. Если мы нашли коэффициенты сплайна, аппроксимирующего поведение кривой между двумя контрольными точками, то такой инструмент OpenGL как evaluator (или функция из семейства glEvalCoord*), может сгенерировать произвольное количество N промежуточных точек ( ). Предполагается, что
). Предполагается, что  пробегает интервал j=1,2,…,N между двумя контрольными точками, а координаты
пробегает интервал j=1,2,…,N между двумя контрольными точками, а координаты 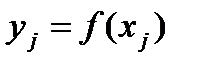 , вычислены с помощью сплайна. Множество сгенерированных вычислителем точек подаются в конвейер OpenGL так, как если бы они были заданы командами glVertex3d. Соединив эти точки (например, по технологии GL_LINE_STRIP), мы получим плавную кривую.
, вычислены с помощью сплайна. Множество сгенерированных вычислителем точек подаются в конвейер OpenGL так, как если бы они были заданы командами glVertex3d. Соединив эти точки (например, по технологии GL_LINE_STRIP), мы получим плавную кривую.


