Вначале вы задаете режим работы с матрицей проецирования — комада
glMatrixMode(GL_PROJECTION);
Затем вы даете команду генерации одной из матриц проецирования. Ниже приведены команды и матрицы, генерируемые с их помощью.
glOrtho (l, r, b, t, n, f); glFrustum (l, r, b, t, n, f);
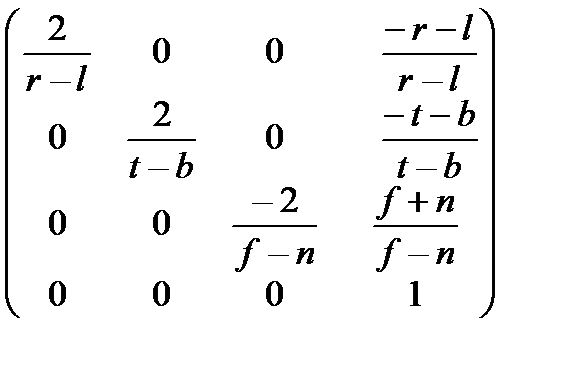

glPerspective (a, k, n, f);

Буквы l, t, r, b, n и f в этих формулах обозначают границы (left, top, right, bottom, near, far) frustum'а. Левая (left), верхняя (top), правая (right), нижняя (bottom), ближняя (near) и дальняя (far) границы frustum'а. Рассмотрим, что происходит с кватернионом  при воздействии на него матрицы glOrtho (l, r, b, t, n, f) — ортографического проецирования
при воздействии на него матрицы glOrtho (l, r, b, t, n, f) — ортографического проецирования
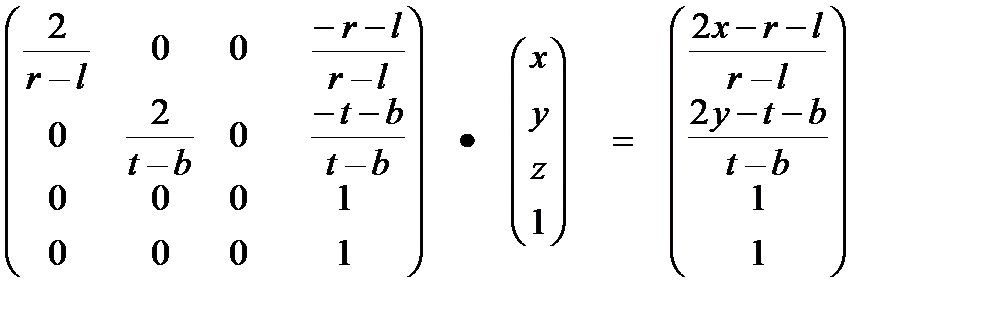
Для того, чтобы оценить результат воздействия матрицы проецирования на вектор  надо подставить вместо x, y, z некоторые граничные значения и отбросить четвертую координату, которая выполняет вспомогательную роль. Например, если вершина находится на правой границе области нормирования (x = right) и в ее центре по вертикали
надо подставить вместо x, y, z некоторые граничные значения и отбросить четвертую координату, которая выполняет вспомогательную роль. Например, если вершина находится на правой границе области нормирования (x = right) и в ее центре по вертикали

то, подставив вместо  вектор
вектор

получим вектор  , который расположен на правой границе двухмерного нормированного пространства. Подставив x, соответствующий левой границе области нормирования, x = left, получим вектор
, который расположен на правой границе двухмерного нормированного пространства. Подставив x, соответствующий левой границе области нормирования, x = left, получим вектор  . Эти векторы задают координаты точек двухмерного нормированного пространства. Третья координата выполняет вспомогательную роль (такую же, какую выполняла четвертая координата в трехмерном пространстве). В качестве упражнения подставьте координаты точек, расположенных на нижней и верхней границах области нормирования:
. Эти векторы задают координаты точек двухмерного нормированного пространства. Третья координата выполняет вспомогательную роль (такую же, какую выполняла четвертая координата в трехмерном пространстве). В качестве упражнения подставьте координаты точек, расположенных на нижней и верхней границах области нормирования:
 и
и 
и убедитесь, что они преобразуются в векторы 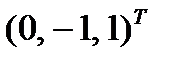 и
и  .
.

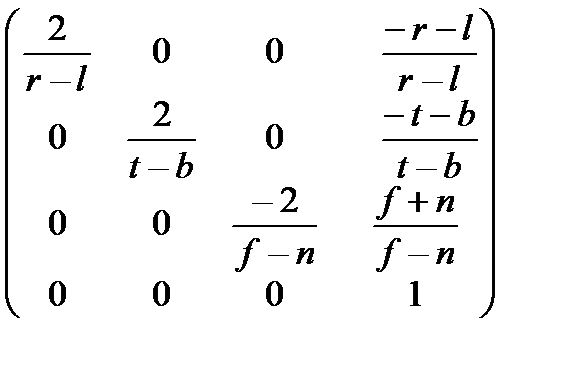


 при воздействии на него матрицы glOrtho (l, r, b, t, n, f) — ортографического проецирования
при воздействии на него матрицы glOrtho (l, r, b, t, n, f) — ортографического проецирования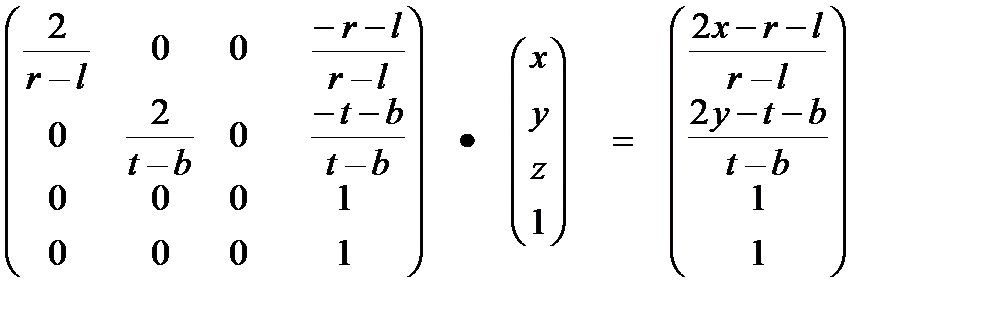


 , который расположен на правой границе двухмерного нормированного пространства. Подставив x, соответствующий левой границе области нормирования, x = left, получим вектор
, который расположен на правой границе двухмерного нормированного пространства. Подставив x, соответствующий левой границе области нормирования, x = left, получим вектор  . Эти векторы задают координаты точек двухмерного нормированного пространства. Третья координата выполняет вспомогательную роль (такую же, какую выполняла четвертая координата в трехмерном пространстве). В качестве упражнения подставьте координаты точек, расположенных на нижней и верхней границах области нормирования:
. Эти векторы задают координаты точек двухмерного нормированного пространства. Третья координата выполняет вспомогательную роль (такую же, какую выполняла четвертая координата в трехмерном пространстве). В качестве упражнения подставьте координаты точек, расположенных на нижней и верхней границах области нормирования: и
и 
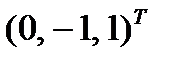 и
и  .
.


