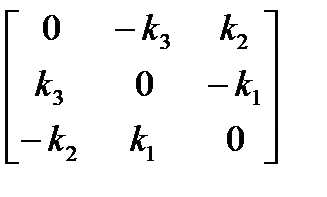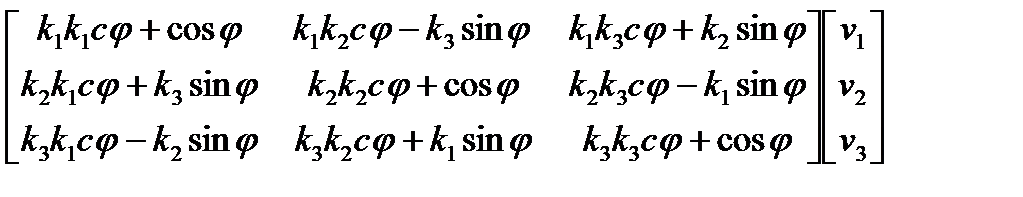Поворот точки в пространстве вокруг произвольной оси
В компьютерной графике принято вычислять новое значение вектора путем умножения старого на матрицу поворота или сдвига. Наша цель — найти коэффициенты матрицы поворота, которая, воздействуя на вектор v, повернет его на угол φ вокруг оси s. Рассмотрим, как изменится вектор при его повороте вокруг некоторой оси s на угол φ.
Начальное положение вектора обозначим буквой v, а конечное — буквой vf (см. рис.). Рассмотрим конец вектора v, как точку трехмерного векторного пространства с началом в точке o. Тогда начальному положению конца вектора v будет соответствовать радиус-вектор r, а конечному rf. Произвольная ось вращения определяется точкой q и направлением s с ортом k. Пусть q есть радиус-вектор точки q. Выполним поворот точки r вокруг оси s на угол φ, отсчитываемый против часовой стрелки, если взгляд направить навстречу вектору s. Плоскость вращения, а, следовательно, и векторы n, nf и b, лежащие в этой плоскости, перпендикулярны оси вращения s. Из рисунка видно, что вектор v можно представить, как разность двух векторов r – q. Этот же вектор можно представить, как сумму других векторов s + n. Манипулируя этими равенствами, попытаемся выразить конечное положение точки rf через исходные величины: r, q и φ. Имеем следующие векторные равенства: n = v – s, s = (v · k) k, // Скалярное произведение (v · k) определяет длину оси вращения s, а орт k — его направление n = v – (v · k) k, rf = q + s + nf При вращении вектор s не изменится, а вектор n повернется на угол φ в сторону вектора b и займет положение nf. Вектор b лежит в плоскости вращения и ортогонален вектору n. Он равен векторному произведению b = k × n. Так как орт k имеет единичную длину, то длина |b| вектора b равна длине вектора |n| (радиусу вращения). Заметим, что векторное произведение других векторов k × v — это вектор, который имеет то же самое направление и длину. Длина равна |k||v|sin(v,k) в силу определения векторного произведения. Так как |v|sin(v,k) = |n|, то справедливы равенства. b = k × n = k × (v – s) = k × (v – (v · k) k) = k × v После поворота на угол φ вектор n станет равным вектору nf = n·cosφ +b·sinφ. В этом можно убедиться, рассматривая следущий рисунок. Учтите, что n, nf и b имеют одинаковую длину, но разные направления. >
После поворота рассматриваемая точка r будет определяться радиус-вектором rf. rf = q + s + nf = q + s + n · cosφ + b · sinφ = = q + (v · k) k + (v – (v · k) k) cosφ + (k × n) sinφ = = q + (v · k) k + cosφ (v – (v · k) k) + sinφ (k × (v – (v · k) k)), Преобразуем выражение (v · k) k. Скалярное произведение (v · k) = (v · k) k = Напомним, что два стоящих рядом вектора kk обозначают операцию диадного произведения векторов, которое является матрицей. Например, диадное произведения произвольных векторов x и y равно: xy = В нашем случае диадное произведение kk есть матрица размерностью 3×3, составленная из компонентов орта оси вращения. Мы приблизились к цели — получить формулу для матрицы поворота. Теперь вектор (v · k) k записан в виде произведения матрицы kk на вектор v. Подставим это выражение в формулу для вычисления rf. rf = q + (v · k) k + cosφ (v – (v · k) k) + sinφ k × v = = q + kk · v + cosφ (v – kk · v) + sinφ k × v = = q + kk · v + cosφ (I – kk) · v + sinφ k × v = q + A · v Матрица A, как было сказано выше, поворачивает вектор v на угол φ вокруг оси s. Ее коэффициенты мы сейчас и пытаемся определить. Распишем в покомпонентном виде векторное произведение k × v. k × v = Заметим, что тот же результат может быть получен путем умножения матрицы (обозначим ее k×) на вектор v. k × v = Подставим матрицу с необычным обозначением k× в развернутое выражение для радиуса-вектора rf. После этого можно выписать выражение для матрицы поворота A. A = (1 – cosφ) kk + cosφ I + sinφ k× Здесь использованы следующие обозначения для матриц. kk = В развернутом виде матрица A будет иметь такой вид. A = Матрица А является ортогональной. Это означает, что при ее транспонировании изменится только знак перед последним ее слагаемым (sinφ k×), что соответствует повороту точки на угол –φ. Окончательное выражение для радиуса-вектора rf (конца вектора v) получим, подставив значение v = r – q. rf = q + A · (r – q) Введем обозначение: cφ = 1 – cosφ и учтем, что на практике достаточно часто ось вращения проходит через начало координат. В этом случае выражение для rf будет иметь более простой вид. rf = A · v =
|

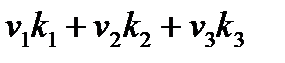 является множителем, который стоит перед вектором k. В покомпонентном виде это произведение имеет вид.
является множителем, который стоит перед вектором k. В покомпонентном виде это произведение имеет вид. = kk · v,
= kk · v,
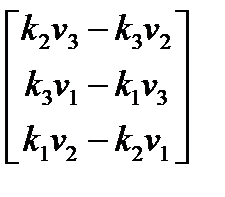
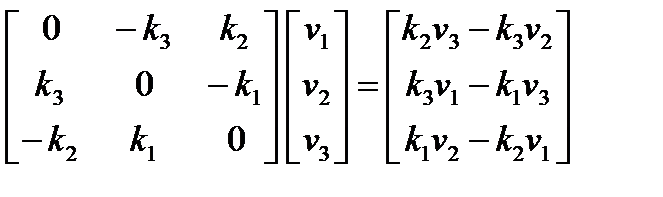
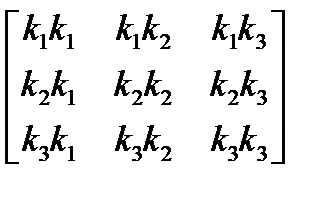 , I =
, I =  , k× =
, k× =