Математические основы компьютерной графики
Положение точек в пространстве принято задавать с помощью тройки чисел (x,y,z) — декартовых координат. Говорят, что точка задана вектором в трехмерной системе координат. Трансформация сцены OpenGL (перемещение или вращение объектов) производится путем аффинных преобразований координат всех точек объекта. Под аффинными преобразованиями имеют в виду: сдвиг, масштабирование, вращение. ¨ Сдвигу точки в пространстве соответствует операция сложения двух векторов:
¨ Вращению точки (например, вокруг оси z) соответствует операция умножения матрицы на вектор: Выведем формулу поворота и соответствующую ей матрицу вращений. Представим, что точку с координатами (
После этого преобразования координаты точки станут (
Хотим получить выражение
Аналогично для координаты y.
Итак, мы получили:
что в матричном виде может быть записано как:
¨ Масштабированию точки также соответствует операция умножения матрицы на вектор. Например, для уменьшения длины вектора в 2 раза (при сохранении его направления) достаточно умножить (справа) вектор на матрицу, в главной диагонали которой стоят коэффициенты 0,5.
Следующая матрица отражает (особым образом масштабирует) точку относительно плоскости OYZ.
Рассмотрим еще один пример трансформации вектора. Для простоты рассмотрим двухмерный, вектор (
Как видите, здесь ненулевые коэффициенты стоят на диагонали, которая противоположна главной. Вращению точки вокруг произвольной оси тоже соответствует операция умножения матрицы на вектор. Вывод этой матрицы потребует несколько больших усилий и мы его приводем ниже, но отметим, что функция glRotate OpenGL умеет создавать такую матрицу. Она требует задать угол и координаты оси, вокруг которой надо произвести вращение. Quaternions (кватернионы) Рассмотренные выше аффинные преобразования сдвига, масштабирования, вращения и отражения можно, как вы убедились, записать в матричной форме. Для вращения (rotate) и масштабирования (scale) надо умножать матрицу на вектор, а для сдвига (translate) надо прибавить вектор смещения. Этот диссонанс не позволяет унифицировать матричные операции конвейера OpenGL. Для его успешной работы необходимо все элементарные преобразования (сдвиг, вращение, масштабирование, отражение) выполнять единым способом. Поэтому математики и разработчики выработали другой способ представления координат точки. Он реализуется с помощью кватернионов (иногда называемых однородными координатами точки). Кватернион — это просто четырехмерный вектор. Четвертая, фиктивная координата нужна лишь для того, чтобы унифицировать преобразования. Смотрите, как можно сдвинуть вектор путем умножения соответствующего ему кватерниона на матрицу размером (4x4).
Этот трюк позволил единым способом производить все типы преобразований координат. Для вращения кватерниона также используется операция умножения на матрицу размером (4x4).
В приведенных формулах четвертая координата w равна единице и не работает (не изменяется в процессе преобразования). Математики придумали, как ее использовать для масштабирования координат. Если задать ей значение, отличное от единицы, то это равносильно делению остальных координат на w. В результате мы получим трехмерный вектор с координатами (x/w, y/w, z/w). Говорят, что трехмерное представление точки (x, y, z, w) есть ее центральная проекция на плоскость w=1. Это трудно представить, так как, вообще, трудно представить четырехмерное пространство. Но вы можете понять, что происходит, снизив размерность пространства, например, выбросив координату z. Важно понять, что теперь координаты двухмерного вектора зависят от величины w.
Трехмерные мировые координаты вершин, из которых собираются объекты сцены OpenGL (на схеме справа), преобразуются в соответствии с приведенной схемой и в конце-концов становятся двухмерными координатами пикселов в пределах Windows-формы (на схеме слева). Цепь преобразований на схеме происходит справа-налево и это соответствует правилу умножения координатных векторов вершин на матрицы преобразований. Оно, как вы знаете, также производится справа-налево. Для удобства преобразований вместо трехмерных векторов евклидова пространства используют четырехмерные векторы (quaternion), которые унифицируют все виды трансформаций изображений: масштабирование, сдвиги и вращения. Например, команда glTranslate (dx, dy, dz); создает матрицу сдвига размерностью (4,4), вид которой мы привели ранее. Четырехмерный вектор мировых координат (quaternion) умножается на нее справа. Результатом является вектор сдвинутый в пространстве на (dx, dy, dz).
Команда glRotate (b, 0, 0, 1); создает матрицу вращения, умножение на которую поворачивает конец вектора вокруг оси z на угол b. Матрица вращения вокруг оси Z рассмотрена ранее.
|


 ) мы хотим повернуть вокруг оси z на угол j.
) мы хотим повернуть вокруг оси z на угол j.
 ). Мы хотим получить вид матрицы вращения, при умножении на которую первый вектор преобразуется во второй. Имеем:
). Мы хотим получить вид матрицы вращения, при умножении на которую первый вектор преобразуется во второй. Имеем:
 .
.

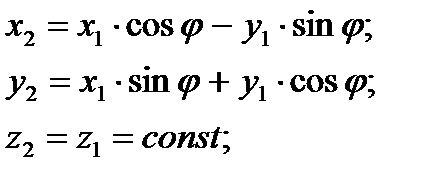



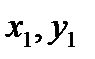 ), описывающий точку на плоскости XY. Для отражения этой точки относительно биссектрисы координатного угла XOY (прямой, проходящей под углом 45°) надо умножить вектор на такую матрицу.
), описывающий точку на плоскости XY. Для отражения этой точки относительно биссектрисы координатного угла XOY (прямой, проходящей под углом 45°) надо умножить вектор на такую матрицу.





