Итерационные методы решения систем уравнений установившегося режима
Общая характеристика методов Методы решения систем уравнений - прямые (точные) и итерационные (приближенные). Прямые применяются для решения систем линейных урав-нений, итерационные - для решения систем линейных и нелинейных уравне-ний. Нелинейные уравнения установившегося режима формируются, если в узлах сети задана постоянная мощность (нагрузка или генерация). Суть итерационных методов: задается некоторое начальное прибли-жение неизвестных U(0), которое постепенно уточняется в ходе выполнения ряда однотипных шагов вычислений (итераций). Если итерационный про-цесс сходится, то получаем искомое решение U(*) с заданной точностью. Итерациями называются многократно повторяющиеся однотипные ша-ги вычислений. Основные характеристики итерационных методов: 1. Условия сходимости к решению, при которых происходит приближе-ние к искомому решению U(*), либо удаление от него; 2. Скорость сходимости. Характеризуется количеством итераций n, необ-ходимых для достижения решения с заданной точностью, или законом изменения вектора погрешности при переходе от итерации к итерации; 2.3. Возможно влияние на скорость сходимос-ти за счет введения дополнительных коэффици-ентов;
4. Необходимость хранения в памяти ЭВМ всех коэффициентов систем уравнений. Удобство программирования, простота алгоритмов и т.д.
Рассматриваем систему нелинейных уравнений установившегося режи-ма. В матричной форме она имеет вид:
В развернутой форме такая система уравнений может быть представлена в следующем виде:
Преобразуем систему (2) квиду, пригодному для решения ее итераци-онными методами. Для этого каждое уравнение системы решим относитель-но одной из неизвестных величин Ui:
Любое i- ое уравнение этой системы можно записать в общем виде:
Если задать начальные приближения неизвестных U(0), подставить их в правую часть уравнений (4) и выполнить необходимые вычисления, опреде-лим следующее приближение неизвестных U(1) и т.д. Такая после-довательность действий соответствует методу простой итерации. Тогда (4) в итерационной форме:
В матричной форме система (3) может быть записана следующим образом:
здесь D - вектор свободных членов, С - матрица коэффициентов при неизвестных, В итерационном виде система (5) принимает вид:
Здесь к – номер приближения неизвестных.
Общий алгоритм итерационных методов решения СНАУ установившегося режима 1) Задание начальных приближений вектора неизвестных U(0)=Uном. Как правило, в качестве начальных приближений напряжений задают номи-нальные напряжения узлов Uном. В некоторых случаях, в качестве начальных приближений напряжений принимают значения, полученные в предыдущих близких расчетах для данной схемы; 2) Задание точности расчета E, предельного количества итераций nпред., начального значения счетчика итераций к= 0 и других параметров расчета; 3) Выполнение итерации в соответствии с формулой (6):
4) Контроль завершения итерационного процесса:
Если условие не выполняется, то изменяем счетчик итераций (к=к+1) и возвращаемся к пункту (3). Повторяем расчет при новых приближениях неизвестных. Если условие выполняется для всех значений Ui, то итерационный процесс завершается, найденные на последней итерации приближения неизвестных U(k+1) принимаются в качестве искомых значений с заданной точностью. Итерационные методы дают последовательность приближенных значе-ний неизвестных, сходящуюся к точному решению. Это означает, что су-ществует предел последовательности:
здесь U(*) - точное решение при Таким образом, точное решение может быть получено лишь в резуль-тате бесконечного итерационного процесса. Всякий вектор U(k), полученный на к- ой итерации, является приближенным решением системы уравнений. Вектор погрешности этого приближенного решения:
Так как точное решение U(*) заранее неизвестно, то о погрешности судят по разности значений на смежных итерациях (к+1) и к, то есть по вектору поправок:
Если
Такой подход к контролю завершения итерационного процесса - не единственный и не очень надежный, так как возможно такое незначительное изменение приближений от итерации к итерации даже вдали от решения. Более строгим и надежным способом контроля завершения итераци-онных процессов является контроль невязок уравнений. Невязка уравнения – разность между левой и правой частями уравнения. Её значение получаем при подстановке в уравнения системы (2) очередного приближения неиз-вестных. Например, для 1-го уравнения:
Для УУР невязка уравнения соответствует расчетному небалансу тока (мощ-ности) в узле. При подстановке точных значений неизвестных U1(*),U2(*),…,Un(*) невязки будут равны нулю:
То есть если итерационный процесс сошелся, то невязки близки к нулю. И чем дальше приближение Ui(k) от точного решения, тем больше величина не-вязок. В общем случае вектор невязок можно определить:
Итерационный процесс сошелся, если выполняются условия завершения итерационного процесса:
Это условие является более надежным критерием окончания итерационного процесса. Достаточным условием сходимости итерационного процесса для урав-нений установившегося режима является:
, i ≠ j.
Т.о. условие сходимости определяется только соотношением элементов матрицы проводимостей Y. В ней диагональные элементы Уіі (собственные проводимости узлов) неравны нулю. Как правило, диагональные элементы матрицы проводимостей больше или равны суммы недиагональных элемен-тов. Т.е. при правильном формировании матрицы, это условие сходимости выполняется всегда.
Два вида сходимости итерационных процессов: 1. Экспоненциальный (апериодический):
2. Колебательный
В случае не сходящихся или расходящихся итерационных процессов, нужно проверять правильность расчетов параметров схемы замещения, правильность расчета элементов и формирования матрицы проводимос-тей, анализировать величины токов и мощностей в заданных узлах.
|

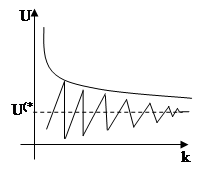 Характер сходимости. Сходимость – апе-риодическая или колебательная.
Характер сходимости. Сходимость – апе-риодическая или колебательная.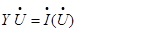 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (4а)
(4а)
 - вектор неизвестных напряжений;
- вектор неизвестных напряжений;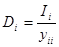 ;
;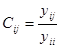 .
. . (6)
. (6) ;
;
 (7)
(7)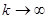 .
. (8)
(8) (9)
(9)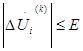 для всех і, то итерационный процесс завершается.
для всех і, то итерационный процесс завершается. . (10)
. (10) .
. (11)
(11) (12)
(12)

 Итерационный процесс может быть так же несходящимся (приб-лижения не приближаются и не удаляются от решения), либо рас-ходящимся (значения приближе-ний удаляются от точного реше-ния).
Итерационный процесс может быть так же несходящимся (приб-лижения не приближаются и не удаляются от решения), либо рас-ходящимся (значения приближе-ний удаляются от точного реше-ния).


