Системы нелинейных уравнений установившегося режима и методы их решения
Нелинейные уравнения установившегося режима получаем в том случае, если нагрузка или генерация в узлах сети задана в виде постоянной мощнос-ти. Математическая модель установившегося режима электрической сети в общем виде представляется как система нелинейных алгебраических урав-нений в форме балансов токов или баланса мощностей с комплексными неиз-вестными и коэффициентами при них. Такие системы уравнений решаются только итерационными методами. В общем виде уравнения установившегося режима можно представить в виде системы неявных функций:
где W - вектор-функция, X и Y - вектор-столбцы независимых и зависимых параметров режима. Независимые параметры X - это заданные параметры режима (P, Q, U). В ходе расчета они остаются неизменными. Зависимые параметры Y – пара-метры режима, которые вычисляются в результате решения системы урав-нений установившегося режима (U΄, U˝, Qi). В состав векторов X и Y могут входить различные параметры режимов в зависимости от постановки задачи, целей расчетов и.д. При расчетах установившегося режима значения элементов вектора X неизменны
Нелинейные уравнения формируются при задании нелинейных источников тока в узлах (генераторы с постоянной мощностью, нагрузки потребителей с постоянной мощностью, нагрузки, заданные статическими характеристика-ми). Постоянная мощность нагрузки или генерации задается в виде узлового тока: I(U) = S* / U*,
где S = const – заданная мощность в узле; U – напряжение в узле; I(U) – нелинейный источник тока.
Тогда СНАУ установившегося режима в форме баланса токов имеет вид:
В матричной форме:
Это система n комплексных уравнений. Систему будем решать методами Зейделя и Ньютона-Рафсона. Из системы (3) в результате несложных преобразований можно получить СНАУ в форме баланса мощности:
где U*диаг – диагональная матрица, на главной диагонали которой размеща- ются сопряжённые комплексы напряжения; Y б - вектор взаимных проводимостей узлов сети с опорным.
U1 = g1(U1, U2, …, Un) U2 = g2(U1, U2, …, Un) ... … … Un = gn(U1, U2, …, Un).
В матричном виде: U = G(U).
В итерационной форме: U(к+1) = G(U(к)).
|

 (1)
(1) , тогда (1) мы можем записать с учетом того, что основ-ной состав элементов вектора Y - это напряжения, т.е.
, тогда (1) мы можем записать с учетом того, что основ-ной состав элементов вектора Y - это напряжения, т.е.  :
: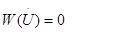 (2)
(2) (3)
(3) .
. (4)
(4) Для решения системы уравнений итерационными методами, её нужно прео-бразовать – решить каждое уравнение относительно одной из неизвестных величин Ui:
Для решения системы уравнений итерационными методами, её нужно прео-бразовать – решить каждое уравнение относительно одной из неизвестных величин Ui:


