Закон Ома в дифференциальной форме
Представим себе электрический ток не в привычном для нас проводнике, а однородной изотропной проводящей среде. В своём направленном движении носители заряда перемещаются по траекториям, которые называются «линии тока». Выделим в среде небольшую поверхность D S. Линии тока, коснувшиеся границы этой поверхности, в дальнейшем вырезают в пространстве «трубку тока» (рис. 6.4.). Особенность этой трубки состоит в том, что заряженные частицы, движущиеся внутри трубки тока, не пересекают её боковую поверхность, то есть они никогда не покидают свою трубку тока.
Рис. 6.4. Выделим в трубке тока два эквипотенциальных сечения D S 1 и D S 2, отстоящие друг от друга на расстоянии D l (рис. 6.5.). Потенциалы этих сечений j1 и j2 = j1 + Dj. Для выделенного элемента трубки тока запишем закон Ома (6.11):
Рис. 6.5. Сократив D S и введя удельную электропроводимость l =
Этот результат становится совсем точным, если перейти к пределу, устремив D l к нулю. Тогда D S = D S 1 = D S 2, так как трубка становится цилиндрической. Кроме того:
Учитывая этот результат, плотность тока запишем так: i = l E, или в векторном виде:
Уравнение (6.13) — математическая запись закона Ома в дифференциальной форме. В этом законе связываются две «локальные» характеристики тока: плотность тока В приведённых рассуждениях есть момент, который не может не настораживать: в законе (6.13) Е — напряжённость электрического поля в проводящей среде с током. А для вычисления этой характеристики мы воспользовались связью напряжённости и потенциала электростатического поля в вакууме (6.12). Однако можно показать, что напряжённость электрического поля внутри однородной проводящей среды совпадает с электростатическим полем, которое существует в вакууме, если обеспечивается то же пространственное распределение потенциала, что и в проводящей среде при наличии тока (см., например, [2]). Теперь на примере расчёта тока утечки в сферическом конденсаторе покажем, как используется закон Ома в дифференциальной форме для решения вполне реальных задач. 3. Пример расчёта силы тока в проводящей среде Пространство между обкладками сферического конденсатора заполнено проводящей средой с удельной электропроводимостью
Рис. 6.6. Задача обладает сферической симметрией. Выделим сферическую эквипотенциальную поверхность радиуса r. Во всех точках этой поверхности не только потенциал одинаков, но и плотность тока по величине одна и та же (6.13): i = l Er, где Er — напряжённость поля в проводящей среде на поверхности выделенной сферы r. Это поле совпадает с электростатическим полем в вакууме при разности потенциалов на обкладках конденсатора U = j1 – j2. Несложно показать, что для сферического конденсатора:
(При выводе этого выражения, можно воспользоваться следующими ранее полученными соотношениями: Теперь, воспользовавшись законом Ома в дифференциальной форме, вычислим плотность тока
и полный ток, протекающий через замкнутую поверхность выделенной сферы:
Величина этого тока не зависит, конечно, от радиуса r выделенной сферической поверхности: I ¹ f (r). Зная закон сохранения электрического заряда, этот результат можно было бы предсказать a priori. Теперь легко вычислить электрическое сопротивление проводящего слоя в конденсаторе:
Нелишне ещё раз напомнить, что здесь
|


 .
.
 , получим:
, получим: .
.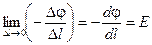 . (6.12)
. (6.12) . (6.13)
. (6.13)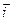 в любой точке пространства и напряжённость электрического поля
в любой точке пространства и напряжённость электрического поля  в той же точке. В соответствии с этим законом, плотность электрического тока прямо пропорциональна напряжённости поля в рассматриваемой точке пространства.
в той же точке. В соответствии с этим законом, плотность электрического тока прямо пропорциональна напряжённости поля в рассматриваемой точке пространства. . Какой ток потечёт в таком конденсаторе, если потенциалы электродов j1 и j2 поддерживать постоянными (рис. 6.6.)?
. Какой ток потечёт в таком конденсаторе, если потенциалы электродов j1 и j2 поддерживать постоянными (рис. 6.6.)?
 .
. (2.19),
(2.19),  (4.8),
(4.8),  (4.5)).
(4.5)).
 .
. .
.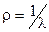 — удельное сопротивление среды, R — сопротивление проводящего слоя, а вот R 1 и R 2 — радиусы сферических обкладок конденсатора.
— удельное сопротивление среды, R — сопротивление проводящего слоя, а вот R 1 и R 2 — радиусы сферических обкладок конденсатора.


