„Мішаний добуток векторів”
Визначити, якою є трійка  ,
,  ,
,  (правою чи лівою), якщо
(правою чи лівою), якщо
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Відповідь: 1)права, 2)ліва, 3)ліва, 4)права, 5)вектори компланарні, 6)ліва.
Обчислити мішаний добуток  :
:
 ;
;  ;
;  ;
;  .
.
Відповідь: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 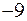 .
.
Знайти мішаний добуток векторів  ,
,  ,
,  і визначити, правою чи лівою є трійка векторів
і визначити, правою чи лівою є трійка векторів  ,
, 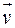 ,
,  . Якою трійкою є трійка векторів
. Якою трійкою є трійка векторів 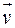 ,
,  ,
,  ?
?
Відповідь: 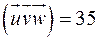 ; трійка векторів
; трійка векторів  ,
, 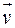 ,
,  – права; трійка векторів
– права; трійка векторів 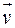 ,
,  ,
,  – ліва.
– ліва.
Вектори  ,
,  ,
,  утворюють праву трійку і взаємно перпендикулярні. Знаючи, що
утворюють праву трійку і взаємно перпендикулярні. Знаючи, що  обчислити
обчислити  .
.
Відповідь:  .
.
Дано три вектора:  ,
,  та
та  . Обчислити
. Обчислити  .
.
Відповідь: 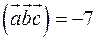 .
.
Вектор  перпендикулярний до векторів
перпендикулярний до векторів  і
і  , кут між векторами
, кут між векторами  і
і  рівний
рівний  . Відомо, що
. Відомо, що  ,
,  ,
,  . Знайдіть
. Знайдіть  .
.
Відповідь: 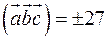 , плюс, коли тріка векторів права, мінус – ліва.
, плюс, коли тріка векторів права, мінус – ліва.
Дано вектори  ,
,  і
і  . Знайдіть: а)
. Знайдіть: а)  ; б)
; б)  ; в)
; в)  .
.
Відповідь:а)  ; б)
; б)  ; в)
; в)  .
.
Встановити, чи компланарні вектори  ,
,  ,
,  , якщо:
, якщо:
1)  ; 2)
; 2)  ;
;
3)  .
.
Відповідь: 1)компланарні; 2)некомпланарні; 3)компланарні.
Встановити, чи компланарні вектори,  ,
, 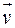 ,
,  , якщо:
, якщо:
1)  ,
,  ,
,  ;
;
2)  ,
,  ,
,  ;
;
3)  ,
, 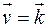 ,
,  , де
, де  ,
,  .
.
Відповідь: 1)ні; 2)ні; 3)так.
Довести, що чотири точки  ,
, 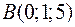 ,
,  ,
,  лежать у одній площині.
лежать у одній площині.
Обчислити об`єм тетраедра, вершини якого знаходяться у точках  ,
,  ,
,  та
та  .
.
Відповідь:  куб. од.
куб. од.
Знайти об`єм трикутної піраміди  :
:
1) 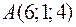 ,
,  ,
,  та
та  ;
;
2)  ,
,  ,
, 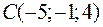 та
та  .
.
Відповідь: 1) 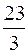 ; 2)
; 2)  .
.
Дано вершини тетраедра:  ,
,  ,
,  та
та  . Знайти довжину його висоти, що опущена з вершини
. Знайти довжину його висоти, що опущена з вершини  .
.
Відповідь:  лін. од.
лін. од.
З`ясувати, чи компланарні вектори  ,
,  ,
,  :
:
 ;
;  ;
; 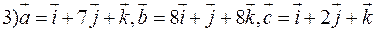
Відповідь: 1)так; 2)ні; 3)так.
Знайти об`єм паралелепіпеда, побудованого на векторах
 ,
,  ,
,  :
: 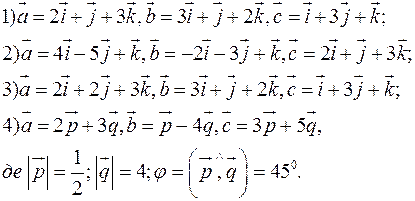
Відповідь: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
Дано паралелепіпед  . Знайти, яку частину об’єму даного паралелепіпеда складає об’єм тетраедра
. Знайти, яку частину об’єму даного паралелепіпеда складає об’єм тетраедра  .
.
Відповідь:  .
.
Об’єм трикутної піраміди дорівнює  куб. од. Три його вершини знаходяться у точках
куб. од. Три його вершини знаходяться у точках 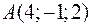 ,
,  ,
,  . Знайти координати четвертої вершини
. Знайти координати четвертої вершини  , якщо відомо, що вона належить осі
, якщо відомо, що вона належить осі  .
.
Відповідь:  .
.
Знайти момент сили  , що прикладена до точки
, що прикладена до точки 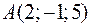 , відносно осі: а)
, відносно осі: а)  ; б)
; б) 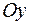 ; в)
; в)  .
.
Відповідь: а)  ; б)
; б)  ; в)
; в)  .
.
В прямокутному паралелепіпеді 
 см,
см,  см,
см,  см. По діагоналі
см. По діагоналі  напрямлена сила
напрямлена сила  , рівна по модулю
, рівна по модулю  . Знайти момент цієї сили відносно точки
. Знайти момент цієї сили відносно точки  та відносно осі
та відносно осі  .
.
Відповідь:  ,
,  . Вказівка: Прийміть вершину
. Вказівка: Прийміть вершину  за початок координат.
за початок координат.
Знайти момент рівнодійної сил  ,
, 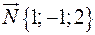 і
і  , прикладених у точці
, прикладених у точці  відносно бісектриси координатного кута площини
відносно бісектриси координатного кута площини 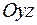 , що розташовані у першій та третій чвертях.
, що розташовані у першій та третій чвертях.
Відповідь:  .
.

 ,
,  ,
,  (правою чи лівою), якщо
(правою чи лівою), якщо ,
,  ,
,  ,
,  ,
,  ,
,  .
. :
: ;
;  ;
;  ;
;  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 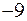 .
. ,
,  ,
,  і визначити, правою чи лівою є трійка векторів
і визначити, правою чи лівою є трійка векторів  ,
, 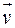 ,
,  . Якою трійкою є трійка векторів
. Якою трійкою є трійка векторів  ?
?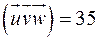 ; трійка векторів
; трійка векторів  обчислити
обчислити  .
. ,
,  та
та  . Обчислити
. Обчислити 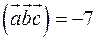 .
. . Відомо, що
. Відомо, що  ,
,  ,
,  . Знайдіть
. Знайдіть 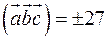 , плюс, коли тріка векторів права, мінус – ліва.
, плюс, коли тріка векторів права, мінус – ліва. ,
,  і
і  . Знайдіть: а)
. Знайдіть: а)  ; в)
; в)  .
. ; б)
; б)  .
. ; 2)
; 2)  ;
; .
. ,
,  ,
,  ;
; ,
,  ,
,  ;
; ,
, 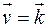 ,
,  , де
, де  ,
,  .
. ,
, 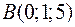 ,
,  ,
,  лежать у одній площині.
лежать у одній площині. ,
,  ,
,  та
та  .
. куб. од.
куб. од. :
: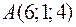 ,
,  ,
,  та
та  ;
; ,
,  ,
, 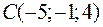 та
та  .
.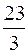 ; 2)
; 2)  .
. ,
,  ,
,  та
та  . Знайти довжину його висоти, що опущена з вершини
. Знайти довжину його висоти, що опущена з вершини  .
. лін. од.
лін. од. ;
;  ;
; 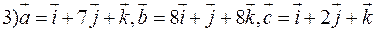
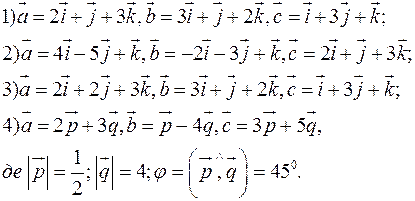
 ; 2)
; 2) 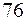 ; 3)
; 3)  ; 4)
; 4)  .
. . Знайти, яку частину об’єму даного паралелепіпеда складає об’єм тетраедра
. Знайти, яку частину об’єму даного паралелепіпеда складає об’єм тетраедра  .
. .
. куб. од. Три його вершини знаходяться у точках
куб. од. Три його вершини знаходяться у точках 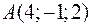 ,
,  ,
,  . Знайти координати четвертої вершини
. Знайти координати четвертої вершини  , якщо відомо, що вона належить осі
, якщо відомо, що вона належить осі  .
. .
.  , що прикладена до точки
, що прикладена до точки 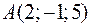 , відносно осі: а)
, відносно осі: а)  ; б)
; б) 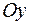 ; в)
; в)  ; б)
; б)  ; в)
; в)  .
. см,
см,  см,
см,  см. По діагоналі
см. По діагоналі  напрямлена сила
напрямлена сила  , рівна по модулю
, рівна по модулю  . Знайти момент цієї сили відносно точки
. Знайти момент цієї сили відносно точки  та відносно осі
та відносно осі  .
. ,
,  . Вказівка: Прийміть вершину
. Вказівка: Прийміть вершину  ,
, 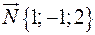 і
і  , прикладених у точці
, прикладених у точці  відносно бісектриси координатного кута площини
відносно бісектриси координатного кута площини 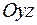 , що розташовані у першій та третій чвертях.
, що розташовані у першій та третій чвертях. .
.


