Властивості векторного добутку.Для довільних векторів 1. 2. 3. Наслідок. Для довільних векторів 1. Які б не були вектори
Знаходження векторного добутку через координати співмножників. Якщо вектори
Геометричний зміст векторного добутку. Площа паралелограма, побудованого на двох векторах. Якщо паралелограм побудовано на векторах Знаходження площі трикутника за координатами вершин. Площа
Застосування векторного добутку. Момент сили. Нехай у деякій точці
Зауваження. Векторний добуток може бути використаний для обчислення моменту сил, що діють на диполь, для обчислення сили, яка діє на провідник зі струмом у магнітному полі і т.д. Підмодуль 2. Мішаний добуток векторів та його властивості.
|
, 
і 
та довільного числа 
мають місце наступні властивості векторного добутку:
= 
;
; 
;
; 
.
має місце співвідношення: 
.
, має місце співвідношення:
.
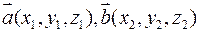, то координати векторного добутку 
знаходять по формулам:
або 
.
тобто S= 
.
:
прикладено силу 
. Моментом сили 
, прикладеної в точці 
(рис.1) називається вектор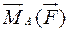 
, який дорівнює векторному добутку радіуса-вектора 
на вектор сили 
