Знаходження об’єму тетраедра по координатам його вершин.
Об’єм тетраедра
2.4. Умова компланарності чотирьох точок. Точки називаються компланарними, якщо вони лежать в одній площині. Для того щоб точки
Питання для самоперевірки. Що називається векторним добутком векторів? Сформулюйте основні властивості векторного добутку. Запишіть формулу обчислення векторного добутку, якщо вектори задано в координатній формі. Як знайти площу трикутника, знаючи координати його вершин? Знайти векторні добутки, якщо
Що називається мішаним добутком векторів? Сформулюйте його основні властивості. Як знайти мішаний добуток, знаючи координати векторів співмножників? У якому випадку мішаний добуток є додатнім числом, а в якому – від’ємним. Наведіть формулу для знаходження об’єму тетраедра за координатами його вершин. Яка умова компланарності чотирьох точок? Як виражається умова компланарності трьох векторів через їх мішаний добуток?
Розділ 2. Аудиторні практичні заняття. Підмодуль 1. Векторний добуток векторів. Питання для перевірки теоретичних знань. 1. Виправте рівність 2. Векторний добуток векторів 3. Як може бути використаний векторний добуток векторів площі паралелограма, побудованого на даних векторах, як на сторонах; площі трикутника, дві сторони якого збігаються з даними векторами Завдання для аудиторної роботи (з розв’язками). 1.Знайти модуль векторного добутку Розв’язання. Відповідь:
2.Обчислити площу паралелограма три вершини якого знаходяться у точках Розв’язання. Нехай Відповідь:
3.Обчислити синус кута утвореного векторами Розв’язання.
Відповідь:
4.Дано трикутник з вершинами
Розв’язання. Щоб розв’язати задачу, достатньо знайти площу трикутника
Відповідь:
5.У прямокутній декартовій системі координат задані дві точки
|

 :
:  .
.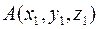 ,
,  ,
,  та
та  лежали в одній площині, необхідно і достатньо, щоб їх координати задовольняли співвідношенню:
лежали в одній площині, необхідно і достатньо, щоб їх координати задовольняли співвідношенню:

 ,
,  ,
,  – взаємно перпендикулярні орти, що утворюють праву трійку:
– взаємно перпендикулярні орти, що утворюють праву трійку: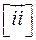 ,
,  ,
, 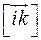 ,
,  ,
,  ,
, 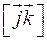 ,
, 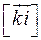 ,
, 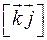 ,
,  .
.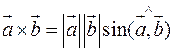 .
. та
та  , якщо вектори задані своїми координатами, обчислюється...
, якщо вектори задані своїми координатами, обчислюється...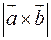 , якщо
, якщо  ,
,  , а кут
, а кут  .
. .
.
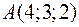 ,
,  ,
, 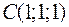 .
. та
та  , тоді
, тоді 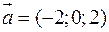 та
та 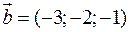 . Площа паралелограма рівна модулю векторного добутку векторів
. Площа паралелограма рівна модулю векторного добутку векторів 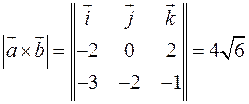 .
. .
.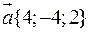 ,
,  .
. , отже
, отже  .
. .
. ;
;  .
. .
. .
. ,
,  ,
,  . Знайти довжину висоти, опущеної з вершини
. Знайти довжину висоти, опущеної з вершини  на сторону
на сторону  .
. та довжину сторони
та довжину сторони  рівна половині площі паралелограма, що побудований на векторах
рівна половині площі паралелограма, що побудований на векторах 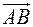 та
та 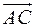 . Знайдемо координати цих векторів та координати їх векторного добутку:
. Знайдемо координати цих векторів та координати їх векторного добутку: 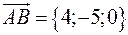 ,
,  ,
, . Оскільки
. Оскільки  , то знаходимо площу паралелограма:
, то знаходимо площу паралелограма:  . Так як
. Так як 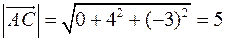 та
та  ,
, 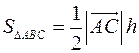 , то
, то  , звідки
, звідки 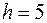 .
.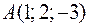 і
і 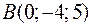 . Знайти на осі
. Знайти на осі 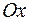 таку точку
таку точку  , щоб площа трикутника
, щоб площа трикутника  кв. од.
кв. од.


