На носители тока на неоднородном участке цепи действуют, кроме электростатических сил  , еще и сторонние силы
, еще и сторонние силы  (рис.2.7). Сторонние силы способны вызывать упорядоченное движение носителей тока так же, как и силы электростатические. На неоднородном участке цепи средняя скорость упорядоченного движения носителей пропорциональна суммарной силе
(рис.2.7). Сторонние силы способны вызывать упорядоченное движение носителей тока так же, как и силы электростатические. На неоднородном участке цепи средняя скорость упорядоченного движения носителей пропорциональна суммарной силе  , тогда плотность тока
, тогда плотность тока
 (2.2)
(2.2)
– это закон Ома для неоднородного участка цепи в дифференциальной форме.
Перейдем к интегральной форме этого закона. Рассмотрим неоднородный участок цепи. Допустим, что внутри этого участка существует линия (контур тока) удовлетворяющая следующим условиям:
1) в каждом сечении, перпендикулярном к контуру, величины 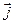 ,
, 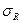 ,
,  и
и  имеют с достаточной точностью одинаковые значения;
имеют с достаточной точностью одинаковые значения;
2) векторы 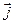 ,
,  ,
,  в каждой точке направлены по касательной к контуру. Поперечное сечение проводника может быть непостоянным.
в каждой точке направлены по касательной к контуру. Поперечное сечение проводника может быть непостоянным.
 Выберем произвольно направление движения по контуру.
Выберем произвольно направление движения по контуру.
Пусть выбранное направление соответствует перемещению от конца 1 к концу 2 участка цепи. Спроектируем выражение (2.2) на элемент контура1-2:
 , (2.3)
, (2.3)
причем 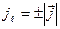 ;
;  ;
;  . Знак «+» берем в том случае, если ток течет от 1 к 2, «-»если ток течет в направлении 2 к 1. Вследствие сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой. Поэтому вдоль контура
. Знак «+» берем в том случае, если ток течет от 1 к 2, «-»если ток течет в направлении 2 к 1. Вследствие сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой. Поэтому вдоль контура  . Силу тока в данном случае нужно рассматривать как алгебраическую величину. Направление 1-2 выбрано произвольно, поэтому, если ток течет в выбранном направлении, его считают положительным, если в направлении 2-1 – отрицательным. Заменим
. Силу тока в данном случае нужно рассматривать как алгебраическую величину. Направление 1-2 выбрано произвольно, поэтому, если ток течет в выбранном направлении, его считают положительным, если в направлении 2-1 – отрицательным. Заменим  ;
;  , тогда из (2.3):
, тогда из (2.3):  .
.
Умножим это выражение на  и проинтегрируем вдоль контура:
и проинтегрируем вдоль контура:

Здесь  – сопротивление всей цепи,
– сопротивление всей цепи,  - разность потенциалов на сопротивление R,
- разность потенциалов на сопротивление R,  - ЭДС, действующая на участке 1,2. Тогда
- ЭДС, действующая на участке 1,2. Тогда  , а ток
, а ток 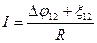 . Это закон Ома для неоднородного участка цепи.
. Это закон Ома для неоднородного участка цепи.
Если цепь замкнутая, то 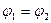 ;
;  . Тогда закон Ома для замкнутой цепи принимает вид:
. Тогда закон Ома для замкнутой цепи принимает вид:  . Если в цепи действует несколько ЭДС, то
. Если в цепи действует несколько ЭДС, то 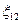 равна их алгебраической сумме.
равна их алгебраической сумме.


 , еще и сторонние силы
, еще и сторонние силы  (рис.2.7). Сторонние силы способны вызывать упорядоченное движение носителей тока так же, как и силы электростатические. На неоднородном участке цепи средняя скорость упорядоченного движения носителей пропорциональна суммарной силе
(рис.2.7). Сторонние силы способны вызывать упорядоченное движение носителей тока так же, как и силы электростатические. На неоднородном участке цепи средняя скорость упорядоченного движения носителей пропорциональна суммарной силе  , тогда плотность тока
, тогда плотность тока (2.2)
(2.2)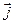 ,
, 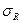 ,
,  и
и  имеют с достаточной точностью одинаковые значения;
имеют с достаточной точностью одинаковые значения; Выберем произвольно направление движения по контуру.
Выберем произвольно направление движения по контуру. , (2.3)
, (2.3)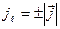 ;
;  ;
;  . Знак «+» берем в том случае, если ток течет от 1 к 2, «-»если ток течет в направлении 2 к 1. Вследствие сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой. Поэтому вдоль контура
. Знак «+» берем в том случае, если ток течет от 1 к 2, «-»если ток течет в направлении 2 к 1. Вследствие сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой. Поэтому вдоль контура  . Силу тока в данном случае нужно рассматривать как алгебраическую величину. Направление 1-2 выбрано произвольно, поэтому, если ток течет в выбранном направлении, его считают положительным, если в направлении 2-1 – отрицательным. Заменим
. Силу тока в данном случае нужно рассматривать как алгебраическую величину. Направление 1-2 выбрано произвольно, поэтому, если ток течет в выбранном направлении, его считают положительным, если в направлении 2-1 – отрицательным. Заменим  ;
;  , тогда из (2.3):
, тогда из (2.3):  .
. и проинтегрируем вдоль контура:
и проинтегрируем вдоль контура:
 – сопротивление всей цепи,
– сопротивление всей цепи,  - разность потенциалов на сопротивление R,
- разность потенциалов на сопротивление R,  - ЭДС, действующая на участке 1,2. Тогда
- ЭДС, действующая на участке 1,2. Тогда  , а ток
, а ток 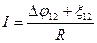 . Это закон Ома для неоднородного участка цепи.
. Это закон Ома для неоднородного участка цепи.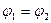 ;
;  . Тогда закон Ома для замкнутой цепи принимает вид:
. Тогда закон Ома для замкнутой цепи принимает вид:  . Если в цепи действует несколько ЭДС, то
. Если в цепи действует несколько ЭДС, то 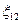 равна их алгебраической сумме.
равна их алгебраической сумме.



