 Закон полного тока, или теорема о циркуляции вектора
Закон полного тока, или теорема о циркуляции вектора  , которая будет рассмотрена ниже, позволяет находить напряженность магнитного поля при наличии симметрии токов без применения закона Био – Савара - Лапласа. Это дает возможность существенно упростить вычисления в ряде случаев.
, которая будет рассмотрена ниже, позволяет находить напряженность магнитного поля при наличии симметрии токов без применения закона Био – Савара - Лапласа. Это дает возможность существенно упростить вычисления в ряде случаев.
Основное отличие магнитного поля от электростатического состоит в том, что магнитное поле непотенциально. Докажем это. Рассмотрим магнитное поле бесконечного прямолинейного проводника с током. Силовые линии (линии напряженности) этого поля представляют собой окружности, плоскости которых перпендикулярны к проводнику, а центры лежат на оси проводника (рис.3.5). Циркуляция вектора  напряженности магнитного поля вдоль произвольной силовой линии L равна
напряженности магнитного поля вдоль произвольной силовой линии L равна
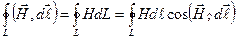 .
.
 При этом L - окружность радиуса r, модуль напряженности по закону Био –Савара-Лапласа равен
При этом L - окружность радиуса r, модуль напряженности по закону Био –Савара-Лапласа равен
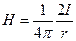 .
.
Вектор  направлен по касательной к окружности, поэтому
направлен по касательной к окружности, поэтому 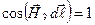 .Тогда
.Тогда
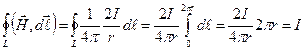 (3.1)
(3.1)
- циркуляция вектора  вдоль силовой линии не равна нулю, следовательно,
вдоль силовой линии не равна нулю, следовательно,
магнитное поле прямолинейного тока непотенциально.
Из выражения (1) следует, что циркуляция вектора  магнитного поля прямолинейного тока одинакова вдоль любой силовой линии и равна силе тока.
магнитного поля прямолинейного тока одинакова вдоль любой силовой линии и равна силе тока.
Формула (3.1) справедлива для замкнутого контура L произвольной формы, охватывающего бесконечно длинный прямолинейный проводник с током I.
Действительно, рассмотрим контур (силовую линию) произвольной формы (рис.3.6). Точка А этого контура находится на расстоянии r от оси проводника с током. Из оси проводника проведем окружность радиуса r через точку А. Тогда вектор  направлен по касательной к этой окружности, следовательно, он перпендикулярен к радиус – вектору
направлен по касательной к этой окружности, следовательно, он перпендикулярен к радиус – вектору  . Элемент силовой линии
. Элемент силовой линии 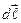 в точке А направлен по касательной к контуру L. Тогда
в точке А направлен по касательной к контуру L. Тогда 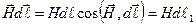 ,
,
где 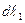 – длина проекции вектора
– длина проекции вектора 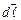 на направление вектора
на направление вектора  . Но малый отрезок
. Но малый отрезок 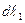 касательной к окружности радиуса r можно заменить дугой этой окружности:
касательной к окружности радиуса r можно заменить дугой этой окружности: 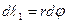 , где
, где  – центральный угол, под которым виден элемент
– центральный угол, под которым виден элемент 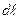 контура L из центра окружности. Тогда:
контура L из центра окружности. Тогда:
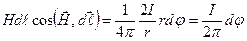 ,
,
 а циркуляция вектора
а циркуляция вектора  равна:
равна:
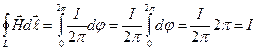 (3.2)
(3.2)
- результат тот же, что и для случая, когда L - окружность.
Таким образом, циркуляция вектора напряженности магнитного поля прямолинейного проводника с током I вдоль замкнутого контура произвольной формы, охватывающего проводник, не зависит от формы контура и численно равна силе тока I.
Рассмотрим случай, когда контур 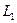 не охватывает проводник с током (рис.3.7). В этом случае циркуляция вектора
не охватывает проводник с током (рис.3.7). В этом случае циркуляция вектора  по контуру L равна сумме циркуляций вектора
по контуру L равна сумме циркуляций вектора  по участку контура 1 a 2 и участку контура 2 b 1, т.е.
по участку контура 1 a 2 и участку контура 2 b 1, т.е.
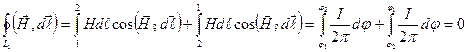 (3.3)
(3.3)
- циркуляция вектора напряженности магнитного поля прямолинейного проводника с током вдоль замкнутого контура, не охватывающего этот проводник, равна нулю.
Можно показать, что формулы (3.2) и (3.3) являются универсальными, т.е. справедливы для проводника любой формы и размеров.
На практике магнитное поле создается, как правило, несколькими проводниками, по которым текут токи 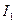 ,
, 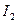 , …,
, …, 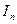 . Каждый проводник с током создает магнитное поле напряженностью
. Каждый проводник с током создает магнитное поле напряженностью  (
( ). Согласно принципу суперпозиции, напряженность результирующего поля равна:
). Согласно принципу суперпозиции, напряженность результирующего поля равна:
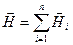 .
.
Циркуляция вектора напряженности  вдоль произвольного замкнутого контура L равна:
вдоль произвольного замкнутого контура L равна:
 .
.
Но, согласно формулам (2) и (3),
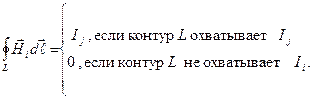
Таким образом,  . (3.4)
. (3.4)
В выражении (3.4) индекс i заменен индексом к для того, чтобы подчеркнуть, что в эту сумму входят только токи, охватываемые контуром L. Формула (3.4) выражает закон полного тока для токов проводимости: циркуляция вектора напряженности магнитного поля постоянного электрического тока вдоль замкнутого контура равна алгебраической сумме токов, охватываемых эти контуром.
Если контур несколько раз охватывает ток, то величина тока учитывается столько раз, сколько раз контур обвивается вокруг тока с учетом направления обхода и знака тока.
Если токи текут непрерывно по поверхности S, то сумму токов  можно заменить интегралом:
можно заменить интегралом:
 ,
,
где 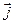 - вектор плотности тока. Тогда закон полного тока (3.4) принимает вид:
- вектор плотности тока. Тогда закон полного тока (3.4) принимает вид:
 ,
,
или
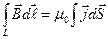 . (3.5)
. (3.5)
Здесь 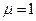 (мы рассматриваем поле в вакууме), L – контур, на который опирается поверхность S. Согласно теореме Стокса
(мы рассматриваем поле в вакууме), L – контур, на который опирается поверхность S. Согласно теореме Стокса 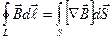 , тогда из (3.5) получаем:
, тогда из (3.5) получаем:
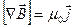 ,
, 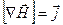 (3.6)
(3.6)
- ротор вектора магнитной индукции 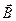 отличен от нуля – магнитное поле непотенциально.
отличен от нуля – магнитное поле непотенциально.
Поле, ротор которого отличен от нуля, называется вихревым или соленоидальным.
Выражение (3.6) представляет собой дифференциальную форму записи закона полного тока.
С помощью закона полного тока (3.6) найдем напряженность магнитного поля внутри соленоида. Пусть длина соленоида много больше его радиуса, 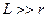 . Такой соленоид можно
. Такой соленоид можно
 считать соленоид бесконечным. Если витки соленоида расположены вплотную или очень близко друг к другу, то соленоид можно приближенно рассматривать как систему большого числа последовательно соединенных круговых токов одинакового радиуса, центры которых лежат на оси соленоида, а плоскости ортогональны ей. Легко видеть, что линии магнитной индукции соленоида параллельны его оси (рис.3. 8). Все поле сосредоточено внутри соленоида, вне соленоида поля нет и
считать соленоид бесконечным. Если витки соленоида расположены вплотную или очень близко друг к другу, то соленоид можно приближенно рассматривать как систему большого числа последовательно соединенных круговых токов одинакового радиуса, центры которых лежат на оси соленоида, а плоскости ортогональны ей. Легко видеть, что линии магнитной индукции соленоида параллельны его оси (рис.3. 8). Все поле сосредоточено внутри соленоида, вне соленоида поля нет и 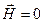 .
.
Для нахождения H выделим участок соленоида длины  , на котором расположено
, на котором расположено 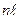 витков, (n - число витков на участке соленоида единичной длины), и проведем контур 1234. Согласно (рис. 3.8) закону полного тока (3.4) имеем:
витков, (n - число витков на участке соленоида единичной длины), и проведем контур 1234. Согласно (рис. 3.8) закону полного тока (3.4) имеем:
 .
.
На участках 1,2 и 3,4 контур перпендикулярен к вектору  , поэтому
, поэтому 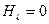 и
и
 .
.
Участок 4,1 находится вне соленоида, следовательно, 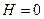 и
и 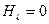 , следовательно,
, следовательно, 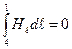 .
.
Тогда 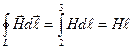 , и
, и 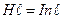 . Сократив на
. Сократив на 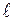 , окончательно получаем:
, окончательно получаем:
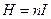 .
.
Из этого выражения видно, что  не зависит ни от расстояния до оси соленоида, ни от размеров самого соленоида. При фиксированном значении силы тока
не зависит ни от расстояния до оси соленоида, ни от размеров самого соленоида. При фиксированном значении силы тока 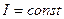 , поле соленоида однородно.
, поле соленоида однородно.
3.7. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ПОСТОЯННЫХ ТОКОВ. ЗАКОН АМПЕРА
Ампер исследовал действие магнитного поля на проводники с током и показал, что сила F, действующая на прямолинейный проводник с током, находящийся в однородном магнитном поле, прямо пропорциональна силе тока I в проводнике, его длине  , магнитной индукции
, магнитной индукции 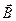 и синусу угла
и синусу угла 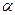 между направлениями тока в проводнике и вектором
между направлениями тока в проводнике и вектором 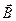 :
:
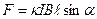 .
.
В случае неоднородного магнитного поля и проводника произвольной формы перейдем к бесконечно малым приращениям, имеем:
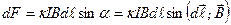 .
.
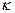 -коэффициент пропорциональности, зависящий от выбора единицы измерения. В СИ
-коэффициент пропорциональности, зависящий от выбора единицы измерения. В СИ 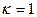 .
.
Будем считать, что элемент проводника 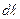 перпендикулярен вектору
перпендикулярен вектору 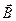 , тогда
, тогда 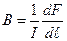 -магнитная индукция
-магнитная индукция 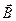 численно равна силе, действующей со стороны поля на единицу длины проводника, по которому течет электрический ток единичной силы и который расположен перпендикулярно к направлению магнитного поля. Т.е. магнитная индукция
численно равна силе, действующей со стороны поля на единицу длины проводника, по которому течет электрический ток единичной силы и который расположен перпендикулярно к направлению магнитного поля. Т.е. магнитная индукция 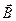 является силовой характеристикой поля.
является силовой характеристикой поля.
Направление силы  определяется по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца расположить по направлению электрического тока в проводнике, то отставленный большой палец укажет направление силы, действующей на проводник со стороны поля.
определяется по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца расположить по направлению электрического тока в проводнике, то отставленный большой палец укажет направление силы, действующей на проводник со стороны поля.
Если 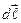 не перпендикулярен
не перпендикулярен 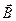 , то вектор
, то вектор  совпадает по направлению с векторным произведением
совпадает по направлению с векторным произведением 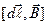 - вектор
- вектор  направлен перпендикулярно к плоскости, образованной векторами
направлен перпендикулярно к плоскости, образованной векторами 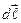 и
и 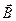 таким образом, чтобы из конца вектора
таким образом, чтобы из конца вектора  вращение от вектора
вращение от вектора 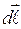 к вектору
к вектору 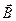 по кратчайшему пути происходило против часовой стрелки.
по кратчайшему пути происходило против часовой стрелки.
Закон Ампера в векторной форме имеет вид:
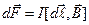 .
.
Силы электромагнитного взаимодействия не являются центральными и всегда перпендикулярны к линиям магнитной индукции.
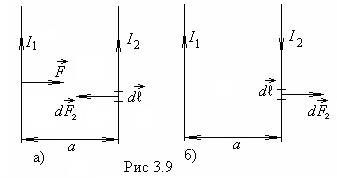 Рассмотрим два длинных прямолинейных проводника, которые расположены параллельно друг к другу. Расстояние между проводниками а. При пропускании тока по проводникам между ними возникает сила взаимодействия. Рассмотрим некоторые частные случаи.
Рассмотрим два длинных прямолинейных проводника, которые расположены параллельно друг к другу. Расстояние между проводниками а. При пропускании тока по проводникам между ними возникает сила взаимодействия. Рассмотрим некоторые частные случаи.
1.Пусть токи 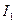 и
и  в проводниках направлены в одну сторону (рис.3.9а). В этом случае проводники притягиваются друг к другу. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на другой проводник. При этом на элемент
в проводниках направлены в одну сторону (рис.3.9а). В этом случае проводники притягиваются друг к другу. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на другой проводник. При этом на элемент 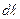 второго проводника с током
второго проводника с током  действует сила
действует сила 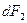 :
:
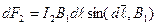 .
.
Если а << 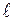 , то проводник можно считать бесконечно длинным, тогда
, то проводник можно считать бесконечно длинным, тогда
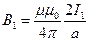 , при этом
, при этом 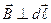 ,
, 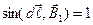 , имеем
, имеем  .
.
Для 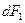 выражение примет такой же вид. Оно симметрично для обоих проводников, поэтому
выражение примет такой же вид. Оно симметрично для обоих проводников, поэтому
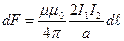 , тогда
, тогда  .
.
2. Если токи противоположны по направлению, то проводники отталкиваются (рис.9б).
 Единицы измерения в системе СИ: магнитная индукция - B =[Тл] – тесла; напряженность магнитного поля H =[
Единицы измерения в системе СИ: магнитная индукция - B =[Тл] – тесла; напряженность магнитного поля H =[  ] - ампер на метр.
] - ампер на метр.
Рассмотрим контур с током, находящийся в магнитном поле. Сила Ампера, действующая на контур, равна 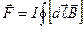 , интегрирование проводится по контуру с током. Если поле однородно, вектор
, интегрирование проводится по контуру с током. Если поле однородно, вектор 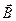 можно вынести за знак интеграла. Интеграл
можно вынести за знак интеграла. Интеграл 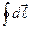 представляет собой замкнутую цепочку элементарных векторов
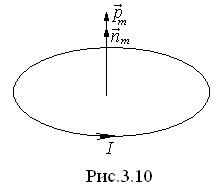
представляет собой замкнутую цепочку элементарных векторов 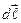 , поэтому он равен нулю. Поэтому результирующая амперова сила равна нулю в однородном магнитном поле. Если же поле неоднородно, результирующая сила отлична от нуля. Рассмотрим плоский контур, размеры которого малы. Такой контур называют элементарным. Его магнитный момент
, поэтому он равен нулю. Поэтому результирующая амперова сила равна нулю в однородном магнитном поле. Если же поле неоднородно, результирующая сила отлична от нуля. Рассмотрим плоский контур, размеры которого малы. Такой контур называют элементарным. Его магнитный момент 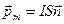 , где
, где 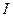 - ток в контуре,
- ток в контуре, 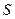 - его площадь,
- его площадь,  - единичный вектор нормали к поверхности контура, связанный с направлением тока правилом правого винта. Сила Ампера, действующая на такой контур в неоднородном магнитном поле, равна
- единичный вектор нормали к поверхности контура, связанный с направлением тока правилом правого винта. Сила Ампера, действующая на такой контур в неоднородном магнитном поле, равна 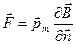 , где
, где 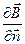 - производная магнитной индукции на направление магнитного момента. Из этой формулы следует:
- производная магнитной индукции на направление магнитного момента. Из этой формулы следует:
1)  в однородном магнитном поле
в однородном магнитном поле 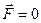 , т.к.
, т.к. 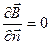 ;
;
2) направление вектора 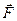 в общем случае не совпадает ни с вектором
в общем случае не совпадает ни с вектором 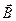 , ни с вектором
, ни с вектором 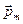 ; вектор
; вектор 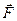 совпадает лишь с направлением элементарного перемещения
совпадает лишь с направлением элементарного перемещения  , взятого в направлении вектора
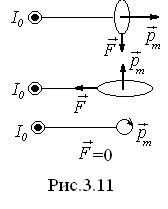
, взятого в направлении вектора 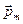 в месте расположения контура. На рис. 3.11 представлены три расположения контура в поле прямого тока. Проекция силы на направление Х равна
в месте расположения контура. На рис. 3.11 представлены три расположения контура в поле прямого тока. Проекция силы на направление Х равна
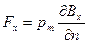 .
.
Найдем момент сил Ампера, действующий на контур с током в магнитном поле. В однородном поле результирующая сил, действующих на контур, равна нулю, следовательно, суммарный момент этих сил не зависит от точки О, относительно которой определяют моменты этих сил. В этом случае говорят просто о моменте амперовых сил. Результирующий момент этих сил 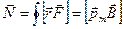 . Таким образом, результирующий момент амперовых сил, действующих на контур с током в однородном магнитном поле, перпендикулярен магнитному моменту контура и вектору магнитной индукции.
. Таким образом, результирующий момент амперовых сил, действующих на контур с током в однородном магнитном поле, перпендикулярен магнитному моменту контура и вектору магнитной индукции.

 Закон полного тока, или теорема о циркуляции вектора
Закон полного тока, или теорема о циркуляции вектора  , которая будет рассмотрена ниже, позволяет находить напряженность магнитного поля при наличии симметрии токов без применения закона Био – Савара - Лапласа. Это дает возможность существенно упростить вычисления в ряде случаев.
, которая будет рассмотрена ниже, позволяет находить напряженность магнитного поля при наличии симметрии токов без применения закона Био – Савара - Лапласа. Это дает возможность существенно упростить вычисления в ряде случаев.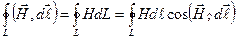 .
. При этом L - окружность радиуса r, модуль напряженности по закону Био –Савара-Лапласа равен
При этом L - окружность радиуса r, модуль напряженности по закону Био –Савара-Лапласа равен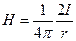 .
.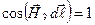 .Тогда
.Тогда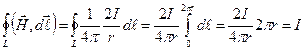 (3.1)
(3.1) . Элемент силовой линии
. Элемент силовой линии 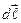 в точке А направлен по касательной к контуру L. Тогда
в точке А направлен по касательной к контуру L. Тогда 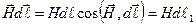 ,
,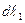 – длина проекции вектора
– длина проекции вектора 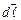 на направление вектора
на направление вектора 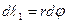 , где
, где  – центральный угол, под которым виден элемент
– центральный угол, под которым виден элемент 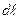 контура L из центра окружности. Тогда:
контура L из центра окружности. Тогда: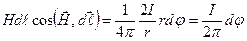 ,
, а циркуляция вектора
а циркуляция вектора 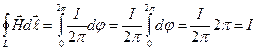 (3.2)
(3.2)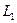 не охватывает проводник с током (рис.3.7). В этом случае циркуляция вектора
не охватывает проводник с током (рис.3.7). В этом случае циркуляция вектора 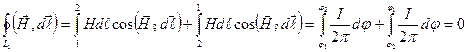 (3.3)
(3.3)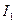 ,
, 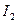 , …,
, …, 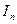 . Каждый проводник с током создает магнитное поле напряженностью
. Каждый проводник с током создает магнитное поле напряженностью  (
( ). Согласно принципу суперпозиции, напряженность результирующего поля равна:
). Согласно принципу суперпозиции, напряженность результирующего поля равна: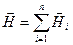 .
. .
.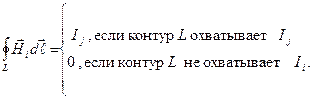
 . (3.4)
. (3.4) можно заменить интегралом:
можно заменить интегралом: ,
,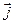 - вектор плотности тока. Тогда закон полного тока (3.4) принимает вид:
- вектор плотности тока. Тогда закон полного тока (3.4) принимает вид: ,
,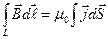 . (3.5)
. (3.5) (мы рассматриваем поле в вакууме), L – контур, на который опирается поверхность S. Согласно теореме Стокса
(мы рассматриваем поле в вакууме), L – контур, на который опирается поверхность S. Согласно теореме Стокса 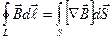 , тогда из (3.5) получаем:
, тогда из (3.5) получаем: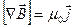 ,
, 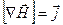 (3.6)
(3.6)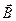 отличен от нуля – магнитное поле непотенциально.
отличен от нуля – магнитное поле непотенциально.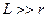 . Такой соленоид можно
. Такой соленоид можно считать соленоид бесконечным. Если витки соленоида расположены вплотную или очень близко друг к другу, то соленоид можно приближенно рассматривать как систему большого числа последовательно соединенных круговых токов одинакового радиуса, центры которых лежат на оси соленоида, а плоскости ортогональны ей. Легко видеть, что линии магнитной индукции соленоида параллельны его оси (рис.3. 8). Все поле сосредоточено внутри соленоида, вне соленоида поля нет и
считать соленоид бесконечным. Если витки соленоида расположены вплотную или очень близко друг к другу, то соленоид можно приближенно рассматривать как систему большого числа последовательно соединенных круговых токов одинакового радиуса, центры которых лежат на оси соленоида, а плоскости ортогональны ей. Легко видеть, что линии магнитной индукции соленоида параллельны его оси (рис.3. 8). Все поле сосредоточено внутри соленоида, вне соленоида поля нет и 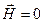 .
. , на котором расположено
, на котором расположено 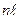 витков, (n - число витков на участке соленоида единичной длины), и проведем контур 1234. Согласно (рис. 3.8) закону полного тока (3.4) имеем:
витков, (n - число витков на участке соленоида единичной длины), и проведем контур 1234. Согласно (рис. 3.8) закону полного тока (3.4) имеем: .
. , поэтому
, поэтому 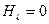 и
и .
.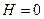 и
и 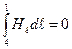 .
.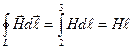 , и
, и 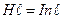 . Сократив на
. Сократив на 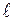 , окончательно получаем:
, окончательно получаем: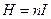 .
.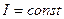 , поле соленоида однородно.
, поле соленоида однородно.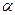 между направлениями тока в проводнике и вектором
между направлениями тока в проводнике и вектором 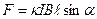 .
.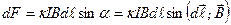 .
.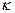 -коэффициент пропорциональности, зависящий от выбора единицы измерения. В СИ
-коэффициент пропорциональности, зависящий от выбора единицы измерения. В СИ 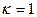 .
.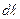 перпендикулярен вектору
перпендикулярен вектору 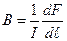 -магнитная индукция
-магнитная индукция  определяется по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца расположить по направлению электрического тока в проводнике, то отставленный большой палец укажет направление силы, действующей на проводник со стороны поля.
определяется по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца расположить по направлению электрического тока в проводнике, то отставленный большой палец укажет направление силы, действующей на проводник со стороны поля.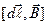 - вектор
- вектор 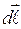 к вектору
к вектору 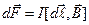 .
. Рассмотрим два длинных прямолинейных проводника, которые расположены параллельно друг к другу. Расстояние между проводниками а. При пропускании тока по проводникам между ними возникает сила взаимодействия. Рассмотрим некоторые частные случаи.
Рассмотрим два длинных прямолинейных проводника, которые расположены параллельно друг к другу. Расстояние между проводниками а. При пропускании тока по проводникам между ними возникает сила взаимодействия. Рассмотрим некоторые частные случаи. в проводниках направлены в одну сторону (рис.3.9а). В этом случае проводники притягиваются друг к другу. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на другой проводник. При этом на элемент
в проводниках направлены в одну сторону (рис.3.9а). В этом случае проводники притягиваются друг к другу. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на другой проводник. При этом на элемент 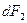 :
: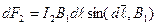 .
.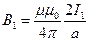 , при этом
, при этом 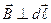 ,
, 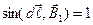 , имеем
, имеем  .
.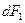 выражение примет такой же вид. Оно симметрично для обоих проводников, поэтому
выражение примет такой же вид. Оно симметрично для обоих проводников, поэтому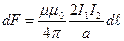 , тогда
, тогда  .
. Единицы измерения в системе СИ: магнитная индукция - B =[Тл] – тесла; напряженность магнитного поля H =[
Единицы измерения в системе СИ: магнитная индукция - B =[Тл] – тесла; напряженность магнитного поля H =[  ] - ампер на метр.
] - ампер на метр.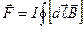 , интегрирование проводится по контуру с током. Если поле однородно, вектор
, интегрирование проводится по контуру с током. Если поле однородно, вектор 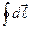 представляет собой замкнутую цепочку элементарных векторов
представляет собой замкнутую цепочку элементарных векторов 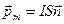 , где
, где 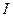 - ток в контуре,
- ток в контуре, 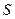 - его площадь,
- его площадь,  - единичный вектор нормали к поверхности контура, связанный с направлением тока правилом правого винта. Сила Ампера, действующая на такой контур в неоднородном магнитном поле, равна
- единичный вектор нормали к поверхности контура, связанный с направлением тока правилом правого винта. Сила Ампера, действующая на такой контур в неоднородном магнитном поле, равна 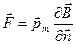 , где
, где 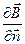 - производная магнитной индукции на направление магнитного момента. Из этой формулы следует:
- производная магнитной индукции на направление магнитного момента. Из этой формулы следует: в однородном магнитном поле
в однородном магнитном поле 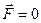 , т.к.
, т.к. 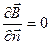 ;
;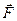 в общем случае не совпадает ни с вектором
в общем случае не совпадает ни с вектором 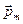 ; вектор
; вектор  , взятого в направлении вектора
, взятого в направлении вектора 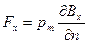 .
.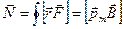 . Таким образом, результирующий момент амперовых сил, действующих на контур с током в однородном магнитном поле, перпендикулярен магнитному моменту контура и вектору магнитной индукции.
. Таким образом, результирующий момент амперовых сил, действующих на контур с током в однородном магнитном поле, перпендикулярен магнитному моменту контура и вектору магнитной индукции.


