 Рассмотрим круговой виток радиуса R, по которому течет ток I (рис. 3.3). По закону Био- Савара- Лапласа индукция
Рассмотрим круговой виток радиуса R, по которому течет ток I (рис. 3.3). По закону Био- Савара- Лапласа индукция 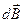 поля, создаваемого в точке О элементом
поля, создаваемого в точке О элементом 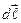 витка с током равна:
витка с током равна:
 ,
,
причём  , поэтому
, поэтому  , и
, и  . С учётом сказанного получаем:
. С учётом сказанного получаем:
 .
.
Все векторы 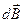 направлены перпендикулярно к плоскости чертежа к нам, поэтому индукция
направлены перпендикулярно к плоскости чертежа к нам, поэтому индукция
 ,
,
напряженность  .
.
Пусть S – площадь, охватываемая круговым витком, 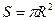 . Тогда магнитная индукция в произвольной точке оси кругового витка с током:
. Тогда магнитная индукция в произвольной точке оси кругового витка с током:
 ,
,
где  – расстояние от точки до поверхности витка. Известно, что
– расстояние от точки до поверхности витка. Известно, что  - магнитный момент витка. Его направление совпадает с вектором
- магнитный момент витка. Его направление совпадает с вектором 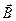 в любой точке на оси витка, поэтому
в любой точке на оси витка, поэтому  , и
, и  .
.
Выражение для  по виду аналогично выражению для электрического смещения в точках поля, лежащих на оси электрического диполя достаточно далеко от него:
по виду аналогично выражению для электрического смещения в точках поля, лежащих на оси электрического диполя достаточно далеко от него:
 .
.
Поэтому магнитное поле кольцевого тока часто рассматривают как магнитное поле некоторого условного «магнитного диполя», положительным (северным) полюсом считают ту сторону плоскости витка, из которой магнитные силовые линии выходят, а отрицательным (южным) – ту, в которую входят.
Для контура тока, имеющего произвольную форму:
 ,
,
где  - единичный вектор внешней нормали к элементу
- единичный вектор внешней нормали к элементу 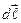 поверхности S, ограниченной контуром. В случае плоского контура поверхность S – плоская и все векторы
поверхности S, ограниченной контуром. В случае плоского контура поверхность S – плоская и все векторы  совпадают.
совпадают.

 Рассмотрим круговой виток радиуса R, по которому течет ток I (рис. 3.3). По закону Био- Савара- Лапласа индукция
Рассмотрим круговой виток радиуса R, по которому течет ток I (рис. 3.3). По закону Био- Савара- Лапласа индукция 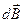 поля, создаваемого в точке О элементом
поля, создаваемого в точке О элементом 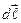 витка с током равна:
витка с током равна: ,
, , поэтому
, поэтому  , и
, и  . С учётом сказанного получаем:
. С учётом сказанного получаем: .
. ,
, .
.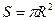 . Тогда магнитная индукция в произвольной точке оси кругового витка с током:
. Тогда магнитная индукция в произвольной точке оси кругового витка с током: ,
, – расстояние от точки до поверхности витка. Известно, что
– расстояние от точки до поверхности витка. Известно, что  - магнитный момент витка. Его направление совпадает с вектором
- магнитный момент витка. Его направление совпадает с вектором 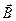 в любой точке на оси витка, поэтому
в любой точке на оси витка, поэтому  , и
, и  .
. по виду аналогично выражению для электрического смещения в точках поля, лежащих на оси электрического диполя достаточно далеко от него:
по виду аналогично выражению для электрического смещения в точках поля, лежащих на оси электрического диполя достаточно далеко от него: .
. ,
, - единичный вектор внешней нормали к элементу
- единичный вектор внешней нормали к элементу 


