ОПИСАНИЕ СРЕДСТВ АНАЛИЗА СИСТЕМ ОДНОВРЕМЕННЫХ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ПАКЕТА GRETL

Рассмотрим процедуру построения системы одновременных уравнений с помощью двухшагового метода наименьших квадратов (2МНК) в пакете Gretl.

Первый способ реализации 2МНК в Gretl осуществляется путём выбора пункта меню Model\Other Linear Models\Two-Stage Least Squares ….

Второй способ – путём выбора пункта Simultaneous Equations меню Model.

В первом случае оценивание каждого уравнения происходит по очереди за один шаг. Во втором – вся система оценивается за одну операцию. Помимо метода 2МНК (TSLS) Simultaneous Equations также предусматривает другие методы оценки, такие как 3МНК (3SLS) и т.д.

Рассмотрим пример структурной модели, представляющей взаимозависимость между объёмом производства и занятостью в химический промышленности Польши 1962-1985гг. (ежегодные данные), модель (5). Для оценивания данной взаимозависимости будем использовать фактор инвестиций.

y1=b12*y2+a13*x3+a14*x4+e1; y2=b21*y1+a21+a22*x2+a23*x3+e2;

(5)

 

 

y₁ - объём производства в химической промышленности за год (produk_t);

y₂ - занятость в химической промышленности (zatrud_t);

x₂ – объём инвестиций в химическую промышленность за год (inwest_t);

x₃ - объём инвестиций предыдущего периода (inwest_t-1);

x₄ - объём производства предыдущего периода (produk_t-1);

Вид данной системы одновременных уравнений – сверхидентифицируемая, т.к. первое уравнение сверх идентифицируемое (H=2)<(D+1=3), второе – точно идентифицируемое (H=2)=(D+1=2), поэтому можем применить 2МНК для оценки её параметров.

 

Откроем набор исходных данных przemysl_chemiczny.gdt (рисунок 1), выбрав пункт меню File\Open Data\Sample file идважды щёлкнув левой кнопкой мыши по названию файла на закладке KUFEL; или создадимprzemysl_chemiczny.gdt, перенеся данные таблицы 1 в файл lab6.xls и импортировав его в пакет Gretl. Для этого в меню Gretl выберем пункт File\Open Data\Import\Excel, в появившемся окне укажем номер строки и столбца начала таблицы Excel и нажмём кнопку ОК, в следующем окне нажмём кнопку YES, затем выберем тип данных временной ряд (time series), нажмём кнопку FORWARD, отметим периодичность данных Annual, нажмём кнопку FORWARD, введём год начала сбора данных 1962, нажмём кнопку FORWARD и ОК.

Сохраним созданный набор данных (рисунок 1) File\Save Data как файл przemysl_chemiczny.gdt на рабочем столе. Данный файл также доступен на сайте www.kufel.torun.pl

Рисунок 1– Набор данных przemysl_chemiczny.gdt

Таблица 1 – Показатели химической промышленности в Польше, 1962-1986гг.

Obs	produk	zatrud	inwest	produk_1	zatrud_1	inwest_1

Удерживая кнопку “Сtrl”, отметим щелчком левой кнопки мыши переменные produk_t (объём производства), zatrud_t (занятость) и inwest_t (объём инвестиций). Затем щелчком правой кнопки мыши вызовем контекстное меню и выберем пункт Time series plot (рисунок 2), нажмём ОК. Характер динамики отмеченных процессов показывает график, представленный на рисунке 3.

 

Рисунок 2 – Построение графика выбранных процессов

Рисунок 3 – Динамика показателей produk_t (объём производства), zatrud_t (занятость) и inwest_t (объём инвестиций).

Как видно из графика за анализируемый период только изменение объёма производства показывает явно выраженную положительную динамику.

Выберем пункт меню Model\Other Linear Models\Two-Stage Least Squares …., что активирует окно спецификации одиночного уравнения. В трёх сегментах окна спецификации при помощи кнопок Choose и Add необходимо определить для отдельного уравнения структурной формы модели (1):

 

Dependent variable – (эндогенную) зависимую переменную (y) в левой части рассматриваемого уравнения;

Independent variables – все переменные в правой части рассматриваемого уравнения.

Instruments – все предопределённые (экзогенные и лаговые эндогенные) переменные всей системы;

 

Как показано на рисунке 4 для первого уравнения укажем:

Dependent variable – y₁ (produk_t);

Independent variables – y₂ (zatrud_t) ,x₃ (inwest_t-1) _, x₄ (produk_t-1);

Instruments – x₂ (inwest_t), x₃ (inwest_t-1) _, x₄ (produk_t-1)и сonst (поскольку x₁ присутствует в системе и равна 1).

 

Как показано на рисунке 5 для второго уравнения укажем:

Dependent variable – y₂ (zatrud_t);

Independent variables – y₁ (produk_t) _, x₂ (inwest_t) _, x₃ (inwest_t-1) и сonst;

Instruments – x₂ (inwest_t), x₃ (inwest_t-1) _, x₄ (produk_t-1)и сonst.

Рисунок 4 – Определение спецификации первого уравнения системы

 

Рисунок 5 – Определение спецификации второго уравнения системы

 

Результаты оценивания рассматриваемой системы с применением 2МНК представлены на рисунках 6 и 7 для первого и второго уравнения соответственно. Структурная форма системы примет вид:

 

y1=-0,097*y2-0,135*x3+1,26*x4+e1; y2=5,137*y1-522,135+0,194*x2-2,32*x3+e2;

 

 

produkt = -0,097* zatrudt -0,135* inwestt-1 +1,26* produkt-1 + e1; zatrudt =5,137* produkt -522,135+0,194* inwestt -2,32* inwestt-1 +e2;

или

 

 

Рисунок 6 – Окно результатов моделирования с применением 2МНК для первого уравнения системы

Рисунок 7 – Окно результатов моделирования с применением 2МНК для второго уравнения системы

 

Результаты оценивания первого уравнения свидетельствуют, что существенное влияние на объём производства (produk_t) оказывают занятость (zatrud_t) и значение объёма производства прошлого периода (produk_t-1), поскольку, согласно t-критерию Стьюдента, параметры при данных переменных являются статистически существенными при уровне значимости 1% (***), т.к. значения p-value 0,046% и 0,001% меньше 1%. В целом модель адекватна при уровне значимости 1%, поскольку для F-критерия Фишера p-value 0,001% меньше 1%.

Результаты оценивания второго уравнения показывают, что существенное влияние на занятость (zatrud_t) оказывают объём производства (produk_t) и объём инвестиций прошлого периода (inwest_t-1). Модель в целом также адекватна.

Исключим из первого уравнения переменную x₃ (inwest_t-1), а из второго - x₂ (inwest_t), поскольку они не оказывают существенного влияния. Система примет вид (6):

y1=b12*y2+a14*x4+e1; y2=b21*y1+a21+a23*x3+e2.

(6)

 

 

Преобразованная система также является сверхидентифицируемой: первое уравнение сверх идентифицируемое (H=2)<(D+1=3), второе – точно идентифицируемое (H=2)=(D+1=2).

Оценим параметры данной системы методом 2МНК вторым способом, обратившись к пункту Simultaneous Equations меню Model. Окно спецификации системы одновременных уравнений представлено на рисунке 8.

 

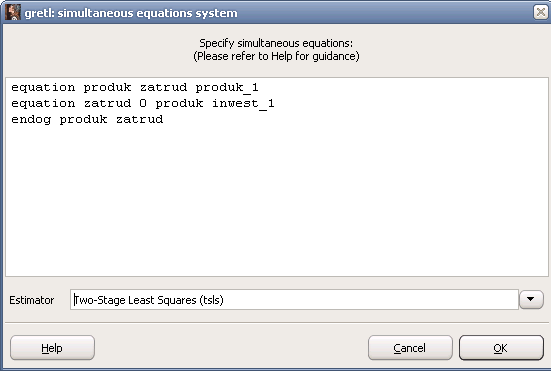
Рисунок 8 - Окно спецификации системы одновременных уравнений

 

Из открывающегося списка внизу окна выберем метод оценки параметров системы – Two-Stage Least Squares (tsls) и правой кнопкой мыши щёлкнем по окну для вызова контекстного меню (рисунок 9).

Выберем пункт контекстного меню Add equation для спецификации первого уравнения системы (6). Затем через пробел введём названия переменных в первом уравнении, щелчком мыши выбирая их из анализируемого набора данных (рисунок 1). Аналогичным образом второй строкой добавим второе уравнение системы. Отметим, что «0» используется для обозначения константы. Затем третьей строкой введём список эндогенных переменных системы (endog), вызвав контекстное меню и выбрав в нём пункт Add list of endogenous variables (рисунок 9).

Рисунок 9 – Вызов контекстного меню

В результате для анализируемой системы (6) спецификация будет иметь вид, представленный на рисунке 10. Нажмём кнопку ОК.

Окно результатов моделирования (рисунок 11) показывает, что все параметры обоих уравнений скорректированной системы значимы по t-критерию Стьюдента при уровне значимости 1%, т.е. все переменные в правой части обоих уравнений оказывают существенное влияние на эндогенные переменные в левой части:

produkt = -0,088* zatrudt +1,2* produkt-1 + e1; zatrudt =5,134* produkt -520,08 -2,14* inwestt-1 +e2;

 

Рисунок 10 – Ввод данных анализируемой модели

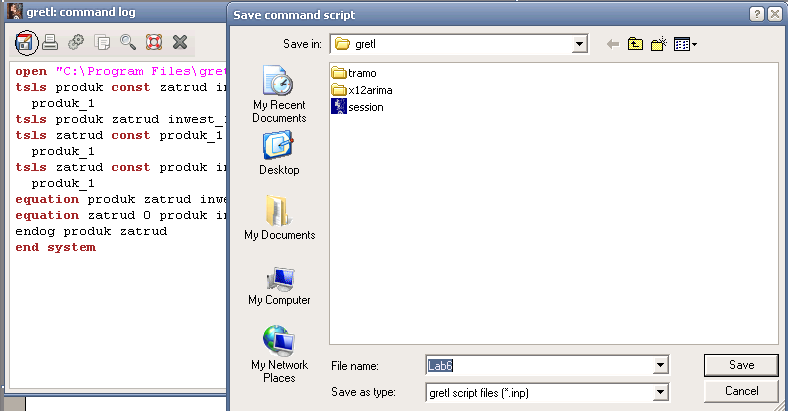
Рисунок 11– Окно результатов моделирования методом 2 МНК (второй способ)

Выберем пункт меню Tools\command log (рисунок 12). В окне command log выводится перечень функций, зарегистрированных в меню команд языка Gretl в процессе оценивания модели. Т.о. существует возможность сохранения всей последовательности действий (показанных выше) по оцениванию рассмотренных систем в виде файла- скрипта формата *.inp. При новом запуске программы Gretl появится возможность открытия и выполнения сохранённого ранее скрипта для получения результатов моделирования, описанных выше.

Рисунок 12 – Вывод перечня функций, зарегистрированных в меню команд

языка Gretl

 

В открывшемся окне command log (рисунок 13) щёлкнем левой кнопкой мыши по иконке меню «сохранить как» (Save as) с изображением дискеты и введём в открывшемся окне название файла-скрипта lab6.inp, по умолчанию сохранив его в папку gretl.

Рисунок 13 – Создание файла– скрипта Lab6.inp

 

Затем выйдем из программы Gretl и запустим её заново. Обратимся к пункту меню File\Script files\User file … (рисунок 14) и выберем сохранённый Lab6.inp.

Рисунок 14 – Открытие файла-скрипта Lab6.inp

 

 

В открывшемся окне выберем иконку меню «выполнить» (run) скрипт (рисунок 15) и в окне script output получим результаты проведённого ранее моделирования.

Рисунок 15 – Выполнение файла-скрипта Lab6.inp