ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ
Многие экономические взаимосвязи допускают моделирование одним уравнением. При этом предполагается, что между независимыми переменными x1…xm и зависимой переменной у существует только прямая связь: xi->y, i=1…m. В такой ситуации зависимая переменная у не оказывает никакого влияния на переменные, входящие в правую часть модели, которые в свою очередь можно изменять независимо друг от друга. В большинстве случаев для оценки таких моделей используется метод 1МНК. Однако, описание сложного экономического процесса предполагает использование системы взаимосвязанных (одновременных) уравнений – simultaneous equations, структурная форма которой представлена формулой (1).
Û BY + AX = E,
где а и b – структурные параметры модели; yi – эндогенная (зависимая) переменная, определяемая внутри модели (i=1…n); xi – предопределённая переменная: экзогенная (независимая) переменная, определяемая вне системы, или лаговая (запаздывающая) эндогенная. В данной системе эндогенные переменные взаимосвязаны, одни и те же эндогенные переменные в одних уравнениях входят в левую часть системы, а в других – в правую, поэтому каждое уравнение не может рассматриваться самостоятельно и для нахождения его параметров традиционный 1МНК неприменим. Для оценивания параметров структурной модели (1) используются следующие методы: • косвенный метод наименьших квадратов (КМНК); • двухшаговый метод наименьших квадратов (2МНК – Two-Stage Least Squares, tsls); • трехшаговый метод наименьших квадратов (3МНК – Three-Stage Least Squares, 3sls); • метод максимального правдоподобия с полной информацией (ММП); • метод максимального правдоподобия при ограниченной информации (ММП). С позиции идентифицируемости структурные модели можно подразделить на три вида: 1. Точно идентифицируемые (все структурные параметры определяются однозначно, единственным образом; для решения системы используется КМНК, 2МНК или 3МНК), D+1=H; 2. Неидентифицируемые (нерешаемы, т.к. один или более параметров не могут быть определены), D+1<H; 3. Сверхидентифицируемые (все структурные параметры определяются, но некоторые из них могут принимать одновременно несколько значений; для решения системы используется 2МНК или 3МНК), D+1>H. Н – число эндогенных переменных в уравнении, D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе. Система линейных функций эндогенных переменных от всех предопределенных переменных системы является приведенной формой модели (2).
............ Û
где pij - коэффициенты приведенной формы модели. Двухшаговый метод наименьших квадратов (2МНК) является наиболее общим и широко распространенным методом решения системы одновременных уравнений, поэтому в ряде компьютерных программ для её решения рассматривается лишь двухшаговый метод наименьших квадратов; пакет Gretl 1.7.1 содержит 2МНК и 3МНК методы. Основная идея 2МНК заключается в том, что на основе приведенной формы модели (2) получают методом 1МНК для каждого i-го (сверхидентифицируемого или идентифицируемого) уравнения системы (1) теоретические значения эндогенных переменных, содержащихся в правой части уравнения
где
Затем, подставив
|

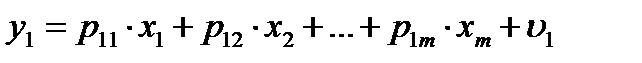
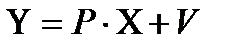 (2)
(2) ,
,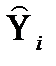 , формула (3).
, формула (3). , (3)
, (3) - матрица значений всех предопределённых переменных системы;
- матрица значений всех предопределённых переменных системы;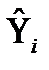 - матрица оценок эндогенных переменных в правой части і-го уравнения;
- матрица оценок эндогенных переменных в правой части і-го уравнения; – подматрица матрицы
– подматрица матрицы  оценок параметров приведенной формы (2), соответствующих эндогенным переменным, включённым в правую часть i-го структурного уравнения (
оценок параметров приведенной формы (2), соответствующих эндогенным переменным, включённым в правую часть i-го структурного уравнения (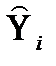 вместо фактических значений
вместо фактических значений 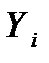 в правой части уравнения, можно применить 1МНК к каждому уравнению структурной формы (1). Т.е. строятся 1МНК оценки структурных параметров
в правой части уравнения, можно применить 1МНК к каждому уравнению структурной формы (1). Т.е. строятся 1МНК оценки структурных параметров 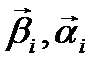 в регрессии (4).
в регрессии (4).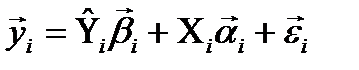 (4) Формула (4) отражает каждое уравнение системы (1) после того как фактические значения эндогенных переменных
(4) Формула (4) отражает каждое уравнение системы (1) после того как фактические значения эндогенных переменных  в правой части были заменены на их теоретические значения (оценки)
в правой части были заменены на их теоретические значения (оценки) 


