Вихідні дані для завдання 2
Нехай γ – кут прокладання нитки (петельний). Тоді з урахуванням довжини крючка е, кут кулірування b к завжди необхідно брати більшим від кута прокладання g, інакше нитка не зможе завестись під крючок голки. Крім того, необхідно враховувати вібрацію нитки в зоні петлетворення, унаслідок яких голка не зможе захопити нитку. Таким чином, якщо не забезпечити між кінцем крючка голки та ниткою деякого проміжку D, то нитка не буде захоплена крючком голки, яка опускається під дією кулірного клина. З вищевикладеного випливає, що при k = 1:
Практично встановлено, що кут c перевищення кута прокладання g у порівнянні з кутом кулірування b к може бути в границях від 5° до 10°. Для цього випадку кут прокладання g повинен бути таким, щоб на момент завершення кулірування голкою нитки вона лише торкалася правої платини. У такому разі:
де hк – задана глибина кулірування; t – голковий крок. Таким чином, при куліруванні для забезпечення одного перегину нитки на петлетвірних органах повинна виконуватись така умова:
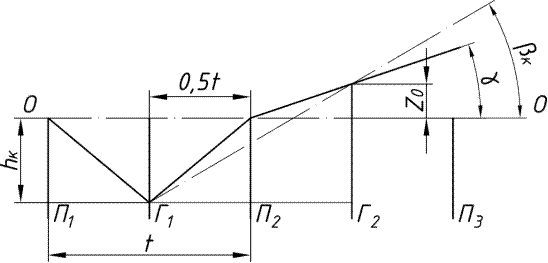
Рисунок 2.1. Розрахункова схема до завдання 2 при k = 1
Рисунок 2.2. Розрахункова схема до завдання 2 при k = 2
При k = 2 нитка буде згинатися не лише голкою, а й правою платиною лише торкаючись другої голки. Оскільки умова Тоді отримаємо таку залежність:
|
.
.
.
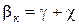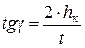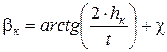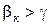завжди виконується автоматично, то в разі, коли k = 2, кут прокладання встановлюють у границях від 25° до 45°.
.
