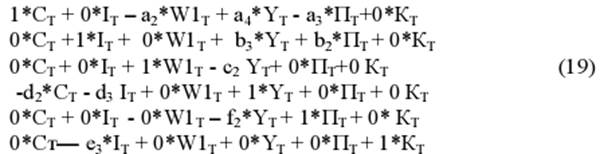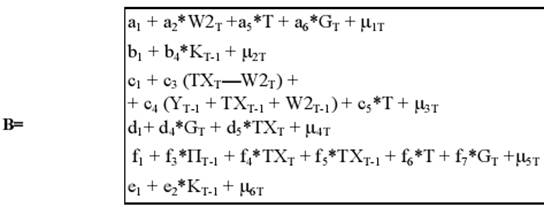Алгоритм численных расчетов

Прежде чем сформулировать алгоритм численных расчетов по предложенной модели, удобно ввести дополнительные матричные обозначения. Перегруппируем переменные в уравнениях (7) – (13) согласно методу Клейна:

В левой части этой системы содержатся все эндогенные переменные, относящиеся к текущему, T-му отрезку времени; правая часть включает запаздывающие эндогенные переменные, управления, константы и случайные возмущения. Левую часть системы можно записать в виде

В матричной записи это можно представить как произведение А*Х, где А обозначает (6х6)-матрицу коэффициентов, а X — вектор-столбец (6x1) выходных переменных. С конкретными значениями матрица А выглядит так:

	C	I	W1	Y	P	K
C	1,000	0,000	-1,221	-0,634	-0,297	0,000
I	0,000	1,000	0,000	-0,100	-0,774	0,000
W1	0,000	0,000	1,000	-0,010	0,000	0,000
Y	-1,685	1,451	0,000	1,000	0,000	0,000
P	0,000	0,000	0,000	0,004	1,000	0,000
K	0,000	-0,814	0,000	0,000	0,000	1,000

А вектор X (вектор-столбец (6x1)) выходных эндогенных переменных имеет вид:

Обозначим через В вектор правых частей уравнений системы (13) - (18):

Система соотношений модели примет тогда вид

А*Х=В. (20)

Чтобы построить траектории эндогенных переменных, надо разрешить это уравнение относительно X при каждом рассматриваемом временном значении Т, т. е. найти

Х = А^-1 *В. (21)

Чтобы вычислить вектор В, надо задать соответствующие значения управлений и получить с помощью специальной подпрограммы реализацию случайного вектора возмущений. После этого по формуле (21) определяются текущие значения эндогенных переменных. Полученные величины используются на последующих итерациях. В этом смысле процесс имитации является замкнутым циклом. В конце каждой итерации выводятся результаты расчетов.

После того как составлена блок-схема вычислений в эксперименте, можно приступить к написанию программы ее реализации на соответствующем алгоритмическом языке. Для этого проведем вычисления в MS EXCEL.

 

План эксперимента

Предположим, что нас интересует влияние 4-х различных типов финансовой политики на такую характеристику функционирования экономики, как национальный доход (в нашем случае валовой региональный продукт). Варианты политики характеризуются соответственно:

1) сохранением на существующем уровне правительственных заказов, правительственного фонда заработной платы и налога,

2) ежегодным снижением налога на 5%,

3) ежегодным увеличением правительственных заказов на 5%,

4) ежегодным увеличением правительственного фонда заработной платы на 5%.

Зададимся целью выбрать политику, обеспечивающую максимальное выборочное среднее валового регионального продукта за следующий прогнозируемый год. Для этого надо провести контрольную серию расчетов (серию 1), в которой все управления фиксированы, а затем просчитать варианты, в которых одно из управлений меняется, а два остальных фиксированы. Серии 2, 3 и 4 соответствуют росту правительственных заказов, правительственного фонда заработной платы и снижению налога.