Системы массового обслуживания
Рассмотрим основные понятия теории систем массового обслуживания, занимающейся построением моделей реальных систем обслуживания, производства, банковской деятельности и т.п. Эти математические схемы характеризуются тем, что в некоторые моменты времени (случайные или детерминированные) возникают заявки на обслуживание и имеются специальные устройства (приборы, инструменты) для обслуживания этих заявок, работающие по определенному закону. Основные понятия теории массового обслуживания: входной поток заявок, обслуживающая система, выходной поток заявок. Входной поток заявок (требований на обслуживание) характеризуется определенной организацией и рядом параметров (рис 9.14): интенсивностью поступления заявок, т.е. числом заявок, в среднем поступивших в единицу времени, и законом распределения вероятностей моментов прихода заявок в систему.
Рис. 9.14. Входной поток заявок Обслуживающая система представляет совокупность устройств (канал, прибор), которые обеспечивают обслуживание заявки, пришедшей в систему. Обслуживающая система характеризуется пропускной способностью (скоростью обслуживания), т.е. числом обслуженных заявок в единицу времени, и законом распределения времени обслуживания заявок. Примерами обслуживающих систем могут служить коммутатор телефонной станции, станок, на котором обрабатываются детали, машины химчистки одежды, оператор сберегательного банка, дежурная справочного бюро и пр. Выходным потоком заявок называется поток обслуженных заявок, выходящих из обслуживающей системы. Параметром выходного потока является интенсивность. Всякая СМО имеет дисциплину очереди, т.е. порядок обслуживания пришедших заявок. Дело в том, что бывают случаи, когда система обслуживания не в состоянии немедленно обслужить все заявки. В результате образуется очередь из заявок, пришедших на обслуживание. То, в каком порядке заявки из очереди будут поступать в обслуживающую систему, определяется дисциплиной очереди. Например, первой заявка поступила и первой обслуживалась; последней заявка поступила и первой обслуживалась; случайный порядок обслуживания заявок; обслуживание определенных заявок в первую очередь (заявки с приоритетом) и т.п. Рассмотрим более детально характеристики входного потока заявок и простейшие СМО. Потоком однородных событий называют временную последовательность появления заявок на обслуживание при условии, что все заявки равноправны. Существуют также потоки неоднородных событий, когда та или иная заявка обладает каким-то приоритетом. Если поток однородный, то каждое событие характеризуется только моментом его наступления tу. Существует два способа задания однородных событий. Первый способ заключается в перечислении всех известных моментов tj. Второй способ заключается в указании зависимости, позволяющей рассчитать tу- по предыдущим значениям. Однако на практике более интересны случайные потоки однородных событий, задаваемые законом распределения, который и характеризует последовательность tj, t2,..., tш или последовательность интервалов между случайными событиями
или для непрерывной случайной величины соответствующая плотность распределения вероятностей
Часто применяется случайный поток событий с ограниченным последействием,т.е. когда случайные величины Е, независимы. Существуют также стационарные потоки,для которых вероятностный режим потока во времени остается неизменным. Это означает, что число заявок, поступивших в СМО в единицу времени, постоянно. Потоком с отсутствием последействия называется такой поток, у которого число заявок, поступивших в данный момент, не зависит от числа заявок, обслуженных в предыдущий момент. Поток с отсутствием последействия — частный случай потока с ограниченным последействием. Для потока без последействия вероятность Р^, t) наступления к событий за интервал (t0, t0 + /) не зависит от возникновения событий до момента /0. Для потоков с ограниченным последействием совместная функция плотности
Стационарный поток с ограниченным последействием характеризуется следующим соотношением:
Это означает, что при j > 1 интервалы имеют одинаковое распределение. Математическое ожидание ц
где \i — средняя длина интервала между последовательными заявками. Для стационарных потоков с ограниченным последействием можно ввести понятие интенсивности потока А, в виде
Эта величина характеризует среднее число событий в единицу времени для данного потока. Примером стационарного потока с ограниченным последействием является поток с равномерным распределением интервалов времени между заявками. Функция плотности f(z) такого потока имеет вид
При этом Такой поток часто используется в практических задачах, возникающих в экономических приложениях. Ординарным потоком называется такой поток, в котором невозможно появление двух и более событий одновременно. В практике часто приходится сталкиваться с групповыми заявками, т.е. несколькими событиями, появляющимися одновременно. Такие потоки не являются ординарными. В теории СМО большое значение имеет так называемый простейший поток однородных событий,называемый потоком Пуассона (пуассоновский поток). Этот поток должен быть стационарным, однородным и без последействия. Для потока Пуассона вероятность Pk(t) наступления события за интервал времени длиной / записывается следующим образом:
где е — основание натурального логарифма,
Функция плотности распределения вероятности этого потока будет
где Для расчетов параметров СМО на основе потока Пуассона необходимо проверить, соответствует ли он закону распределения Пуассона. Признак потока Пуассона — равенство математического ожидания X дисперсии G, т.е. X = G. Пусть х — число заявок, поступивших за единицу времени, т — число единиц времени, an — общее число поступивших заявок. Пример. Проверить, является ли поток требований в систему распределенным по закону Пуассона.
Отсюда Дисперсия потока равна
В связи с тем что Простейший поток и поток с равномерным распределением интервалов времени между последовательными событиями наиболее часто применяются в теории и практике СМО. Часто используется также ординарный стационарный поток с отсутствием последействия, который называется потоком Эрланга. Потоком Эрланга порядка т называют поток, для которого
где Поток событий называется регулярным,если длина интервала между событиями — постоянная величина. Примерами такого потока могут служить ежедневные сводки о каких-либо событиях (отчеты о дневной выручке в магазине, ежедневная сумма сделок на бирже или прихода средств в банк и т.п.), регламентированный поток деталей, сходящих с конвейера, поток поездов в метро и др. Если известна длина интервала регулярного потока а, то такой поток полностью определен во времени и не является случайным. Регулярный поток также является ординарным и стационарным. Однако регулярный поток является потоком с последействием. Интенсивность регулярного потока
Потоки событий различного вида могут разрежаться и объединяться [37]. К сожалению, эти термины могут применяться только к потокам определенного вида. Так, например, если интервалы в потоке Эрланга п -го порядка уменьшить в (я + 1) раз, то интенсивность полученного потока станет равной интенсивности исходного пуассоновского потока, и с ростом я такой поток становится сколь угодно близким к регулярному с той же интенсивностью. Такие нормированные потоки Эрланга дают различные типы потоков с последействием, начиная от потоков без последействия (я = 1) и кончая регулярными (я = °°). Если объединяются несколько независимых ординарных потоков с сопоставимыми интенсивностями, то с ростом числа слагаемых потоков объединенный поток приближается к простейшему с возможной нестационарностью. Если слагаемые потоки стационарны, то в пределе получается пуассоновский поток. Интенсивность объединенного потока равна сумме интенсивностей каждого из них. Поток, получаемый в результате случайного разрежения или объединения пуассоновских потоков, также является пуассоновским. Как будет показано ниже, используя потоки Эрланга и Пуассона, можно рассчитать аналитически установившиеся значения различных параметров СМО. Однако применение этих потоков в практике имитационного моделирования в чистом виде, без специальной корректировки, учитывающей изменения типа потока, его интенсивности и т.п. крайне ограничено. Таким образом, вышеприведенные математические описания потоков однородных событий позволяют формализовать процессы функционирования СМО. Представим СМО в виде п параллельных линий одновременного обслуживания заявок (рис. 9.15).
Рис. 9.15. СМО из п линий обслуживания При поступлении заявок в СМО последняя может находиться в следующих состояниях: все линии (каналы) заняты и имеется свободная линия (канал). Пусть /ож — время ожидания обслуживания, тогда в первом случае поступившая заявка может иметь три варианта поведения, а именно: покинуть систему (/ож = 0), встать в очередь на обслуживание до того момента, пока не освободится свободный канал (/ож = °°) и, наконец, встать в очередь с ограничением времени ожидания обслуживания Исходя из этого СМО подразделяются на системы с отказами Рассмотрим теперь время обслуживания заявки (время занятости линии) to6c как параметр обслуживающей системы. Время обслуживания требований — случайная величина и может изменяться в большом диапазоне. Случайная величина to6c характеризуется законом распределения, который может определяться на основе статистических испытаний. На практике часто исходят из гипотезы о показательном законе распределения времени обслуживания. При показательном законе распределения времени обслуживания функция его распределения Р, равна
где
где 7"обс — среднее время обслуживания одного требования одним обслуживающим устройством. При показательном законе распределения времени обслуживания и при наличии п обслуживающих линий одинаковой мощности
Важным параметром СМО является коэффициент загрузки а
Величина
В противном случае очередь будет бесконечно расти. Ниже приведены расчетные формулы для определения важнейших характеристик качества функционирования СМО при показательном законе распределения времени обслуживания заявок. 1. Вероятность того, что все обслуживающие системы свободны
2. Вероятность того, что все обслуживающие устройства заняты
3. Среднее число устройств, свободных от обслуживания
4. Коэффициент простоя обслуживающих устройств
5. Среднее число устройств, занятых обслуживанием
6. Коэффициент загрузки системы
7. Средняя длина очереди
8. Среднее время ожидания требований в очереди
или
где а — коэффициент загрузки; п — число обслуживающих устройств; То6с — среднее время обслуживания одного требования одним устройством; 0 — интенсивность обслуживания одного требования одним устройством. Таким образом, для простейших потоков и элементарных СМО можно аналитически вычислить их качественные параметры. Реальные экономические объекты, как правило, представляют сложные СМО как по структуре, так и по входным потокам и параметрам. В большинстве случаев аналитические выражения для оценки качества СМО, моделирующих реальные экономические объекты и процессы, найти не удается. Применение имитационного метода к задачам массового обслуживания позволяет находить необходимые показатели качества для экономических систем любой сложности, если удается построить алгоритмы имитации каждой части СМО. Сущность имитационного моделирования СМО заключается в том, что необходимо построить алгоритмы, вырабатывающие случайные реализации заданных событий или потоков. Это означает, что нужно проимитировать все входные потоки, задать случайные значения времен обслуживания заявок для каждого канала и дисциплину очереди. Работа алгоритма заключается в многократном воспроизведении случайных реализаций процесса прихода заявок и процесса их обслуживания при фиксированных условиях задачи. Меняя условия задачи, параметры входных потоков и элементов СМО, можно получить качественные параметры данной СМО при тех или иных изменениях. Качественные параметры СМО типа вышеперечисленных для простейших входных потоков и элементарных СМО оцениваются путем статистической обработки величин, являющихся качественными показателями функционирования СМО. Метод имитационного моделирования позволяет изучать переходные процессы в СМО, возникающие при существенных изменениях распределения моментов поступления заявок в СМО, от преобразования структуры и параметров СМО и т.п. При осуществлении имитационного моделирования стационарный или установившийся режим деятельности СМО наступает после значительного числа имитационных реализаций, а начальные реализации процесса могут существенно отличаться от установившихся. Здесь сразу просматриваются преимущества имитационного метода в отличие от аналитических методов расчета параметров СМО, так как последние позволяют получить величины параметров только для установившихся значений. Рассмотрим методику имитационного моделирования СМО. Вопросы формирования случайных потоков событий Выше были показаны способы применения простейших случайных потоков событий. Как правило, такие потоки должны обладать свойствами стационарности, у них отсутствует последействие и однородность. Если выполнить все эти условия, то имитационное моделирование СМО в отличие от аналитического решения сможет дать дополнительно только значения качественных параметров в переходном процессе, т.е. в начальный период функционирования СМО. Установившиеся значения с точностью до инструментальной ошибки должны быть одинаковы. В учебном процессе при иллюстрации аналитического решения или решения на имитационной модели в большинстве случаев именно так и поступают. Тем самым создается ошибочное впечатление о больших возможностях аналитического или имитационного методов оценки СМО. Причина такого заблуждения заключается в том, что модели СМО строят обычно математики, которым гораздо проще сделать поток однородным, стационарным и без последействия, чем изучать фактические потоки событий в реальных объектах при их моделировании с применением СМО. Способов получения простейших случайных потоков однородных событий, обладающих свойствами стационарности при отсутствии последействия, достаточно много, как и литературы по этому поводу, например работы [19, 43, 37]. Вместе с тем можно утверждать, что применение простейших потоков случайных событий при аналитическом или имитационном моделировании на основе СМО сложных экономических объектов неэффективно и, как правило, создает ошибочное представление о качестве функционирования объекта. В качестве примера рассмотрим сравнительно простую модель СМО фабрики химчистки одежды. Пусть фабрика химчистки имеет 10 машин для чистки одежды. Машины работают две смены —16 ч. В среднем одна машина обрабатывает 5 заказов за 1 ч, 80 заказов за две смены в день. Все 10 машин за 2 смены обрабатывают 800 заказов. В среднем за день на фабрику поступает от 500 до 1500 заказов. Требуется определить оптимальное число работающих машин, длины очередей клиентов и среднее время нахождения в очереди. Используя введенные выше зависимости, можно вычислить значения среднего числа машин химчистки, свободных от работы No, среднюю длину очереди клиентов L и среднее время ожидания клиентов в очереди /ож. Естественно, что для единицу времени служивания одного заказа
число машин, которое необходимо иметь, чтобы обслужить за сутки (сутки приняты за единицу времени) все поступившие заказы. Таким образом, необходимо иметь всего 6,2 машины для случая \1 = 500, а для Х2 = 1500 необходимое число машин составит более 18 (а2 = 18,75). Чтобы очередь заказчиков не росла безгранично, необходимо выполнить условие ки. Поскольку в нашем примере на фабрике имеется 10 машин химчистки, то Следовательно, для входного потока с Каковы же выводы? Мы не будем рассчитывать другие показатели качества обслуживания, так как это заняло бы для нашей небольшой экономической системы достаточно много времени и отвлекло от главного. Выводы таковы: 1. Мы не можем сказать, сколько машин химчистки нужно установить, чтобы обслуживать потоки с Xi = 500 и Х2 = 1500, так как а меняется от 6,2 до 18,75. 2. В связи с тем что потоки заявок в системе рассчитаны для средних суток, то расчеты длины очереди L и среднего времени ожидания обслуживания Тож, как и другие качественные параметры, будут сделаны неверно, так как интенсивность потока в различные часы суток различна и может меняться до 5 раз. Конечно, можно рассчитать эти параметры за каждый час отдельно, но и это будет неверно, так как СМО будет находиться в постоянном переходном процессе. В этом случае входной поток будет нестационарным и с последействием, так как математическое ожидание числа заказов в единицу времени будет меняться в 3—5 раз, а число заказов, поступивших, например, в 18 часов, зависит от того, сколько их было фактически за каждый предыдущий час. 3. Цикл работы фабрики химчистки равен одному году, так как услуги химчистки обладают существенной сезонностью. Имеют место весенний и осенний пики потока заказов, а летом и зимой интенсивность заказов снижается. Весной одежду меняют с зимней на летнюю, а осенью — наоборот. Расчет по средней интенсивности потока заказов ничего хорошего не дает, так как в пик будет перегрузка, а в спад недогрузка. Разница между ними составляет опять же 3—5 раз. 4. Кроме того, имеет место цикличность работы и в зависимости от дня недели и в течение каждого дня. Общий вывод таков:ни один параметр обслуживающей системы (химчистки) не будет найден достоверно как при аналитических расчетах, так и при имитационных, если будут использованы входные потоки Пуассона, обладающие стационарностью, однородностью и отсутствием последействия. Поэтому использование входных потоков такого вида или даже модифицированных в реальных расчетах в чистом виде неприемлемо. Это означает, что если используется какой-то входной поток, закон распределения которого можно записать в аналитической форме, то он должен быть, по крайней мере, преобразован в поток, учитывающий все необходимые факторы, воздействующие на данную СМО. После этого он становится неоднородным, нестационарным с последействием и даже неординарным. Модель формирования такого потока для нашего примера представлена на рис. 9.16.
Рис. 9.16. Модель формирования реального потока заказов фабрики химчистки Если взять поток Пуассона, то вероятность поступления за время t ровно к заявок будет
Блоки 2—4 модели должны воздействовать на параметры Вид конкретной зависимости может быть задан как аналитически, так и таблично или при помощи логических фраз. Только после такого преобразования входного потока можно приступать к имитационному моделированию, например, фабрики химчистки. Выбор размерности входного потока заявок имеет принципиальное значение при его моделировании. Так, например, выбранная для фабрики химчистки размерность, характеризующая ее интенсивность, — число заказов в сутки. Такая размерность не позволяет учитывать изменения интенсивности потока в течение суток, а поэтому не верна. Правильная для нашего случая размерность входного потока заявок на обслуживание должна учитывать тот интервал времени, за который могут произойти какие-либо изменения входного потока и, в частности, его интенсивности. Для нашего случая размерностью должно быть число заказов в час. Существует также еще один способ получения реальных входных потоков. Это использование реальных статистических данных о числе заявок, поступивших в систему за определенное время. Вполне естественно требование, чтобы временной период не был меньше необходимой продолжительности цикла моделирования. Вместе с тем при таком способе формирования входного потока событий возникают проблемы, связанные с воздействием объекта моделирования на входной поток. Фабрика химчистки обладает конечной мощностью, и в период перегрузки каналов очередь заявок на обслуживание обрезается искусственно — прекращается прием заказов на фабрике. Такие факты нужно как-то учитывать, например, путем добавления потерянных заявок в пиковый период, либо согласиться с тем, что модель данной СМО будет с ограничением длины очереди. Для других объектов таких ограничений может и не быть, поэтому прежде чем использовать фактическую статистику, необходимо ее проанализировать на предмет возможного влияния объекта моделирования на входной поток. Входные потоки можно получать также и опросным путем, например, изучая спрос на товары и услуги. Исследование статистических данных для оценки возможности их применения при формировании входных потоков сводится к проведению анализа соответствующего динамического ряда на наличие тренда, сезонности и случайной составляющей. Обычно их отфильтровывают, измеряют и лишь затем формируют необходимый входной поток. Таким же образом поступают при формировании входных потоков из простейшего потока. Полученные составляющие ряда применяются при формировании модели входного потока в соответствии с рис. 5.1.3. Для нашего примера продолжительность моделируемого цикла не может быть меньше одного года, а имитационные реализации должны учитывать данные за каждый час работы фабрики. Только при этих условиях можно получить достоверные качественные показатели, которые не будут одинаковыми в пределах моделируемого цикла. Они будут соответствовать реальным значениям в каждом однотипном интервале времени. Учитывая среднюю длину очереди L, среднее время ожидания обслуживания, а также число фактически загруженных каналов, можно спроектировать, например, такую фабрику химчистки, у которой эти параметры соответствуют желаемым целевым показателям. В п. 5.2 показана агрегативная модель СМО, отображающая производственный процесс, в том числе и процесс функционирования рассмотренной фабрики химчистки. Для различных экономических объектов выбор цикла моделирования может быть другим, но он должен учитывать все или почти все факторы, изменяющие входной поток. Естественно, что для других экономических объектов модель формирования потока Р£ор(7) будет иной, так как экономические факторы могут быть другими. Однако использование потоков без коррекции, как правило, не дает нужных результатов. Аналогичное заключение можно сделать для показателей интенсивности обслуживания 6 и числа обслуживающих каналов. Эти показатели также подвергаются воздействию различных экономических факторов, которые следует учитывать. Например, число каналов обслуживания не может быть постоянной величиной, так как они в реальной жизни выходят из строя, становятся на профилактику, дублируют друг друга и пр. Меняется также их производительность. В этой связи необходимо обратить внимание на то, что фактически ни одна СМО, моделирующая реальные объекты и процессы, не будет находиться в режиме завершенного переходного процесса или в установившемся режиме. Этот факт еще раз подтверждает неэффективность аналитического вычисления качественных параметров СМО для реальных систем. Оценка установившихся значений качественных показателей для СМО, моделирующих реальные экономические системы имитационным способом, также проблематична. Здесь можно говорить о наличии тех или иных близких между собой значениях качественных показателей на определенных участках общего цикла моделирования. Однако говорить что-то об установившихся значениях в общем виде беспредметно. Это можно делать лишь для конкретного объекта.
По принципу работы модели можно разделить на математические и имитационные. Математические модели описывают объект с помощью математических формул, по которым выходные параметры вычисляются на основании значений входных параметров. Имитационные модели имитируют действия, выполняемые объектом, и выходные параметры получаются как результат этих действий. Осуществлять моделирование можно как с помощью физической имитации процессов, так и с помощью программных средств ЭВМ. Второй способ, естественно, является наиболее предпочтительным с точки зрения времени и затрат на построение модели и проведение экспериментов с ней. В настоящее время под термином “имитационная модель”, как правило, понимают именно специальный программный продукт, позволяющий имитировать заданный процесс.
ПРИМЕНЕНИЕ ИМИТАЦИОННОЙ МОДЕЛИ КЛЕЙНА ДЛЯ ПРОГНОЗИРОВАНИЯ ЭКОНОМИЧЕСКОГО РАЗВИТИЯ РЕГИОНА Постановка задачи Мы будем моделировать влияние правительственной финансовой политики на функционирование экономики региона по методу Клейна [1]. Рассмотрим влияние следующих экзогенных переменных: 1) правительственного фонда заработной платы, 2) правительственных заказов 3) налога на деловую активность на следующие эндогенные переменные: 1) личное потребление, 2) заработная плата, 3) прибыли, 4) инвестиции, 5) основной капитал и 6) национальный доход. Описание модели Из сказанного выше следует, что модель должна отражать зависимость 6 перечисленных эндогенных переменных от 3 факторов, определяющих финансовую политику. Стоит отметить, что реалистичная модель, описывающая поведение этих 6 переменных, по-видимому, должна быть значительно более сложной. Поэтому рабочие модели экономики США, такие, как Уортонская и Брукингская, содержат порядка 100 уравнений [1]. Интересующие нас величины зависят от множества других управлений, эндогенных и экзогенных переменных. Однако для иллюстрации достаточно разобрать менее сложную модель экономики США, созданную Клейном [2] и состоящую всего из 6 уравнений. Эта модель обладает двумя хорошими качествами. Во-первых, она относительно проста и легко поддается интерпретации. Во-вторых, хотя для некоторых ее вариантов удается получить аналитическое решение, ей присущи многие свойства более сложных эконометрических моделей, не допускающих непосредственного аналитического исследования. Перечислим управления, эндогенные переменные, уравнения функционирования и тождества модели. Управления W2T — правительственный фонд заработной платы на Т-м отрезке времени (в качестве данных по этой переменной был взят фонд заработной платы органов управления по кварталам), GT — правительственные заказы на Т-м отрезке времени (в качестве этих данных был взят объем госзаказа по Алтайскому краю), ТХT — налог на деловую активность на Т-м отрезке времени (в качестве этих данных была взята сумма поступлений от налогов на прибыль юридических лиц). Эндогенные переменные СT — потребление на Т-м отрезке времени, W1T — фонд заработной платы в частном секторе на Т-м отрезке времени, ПT — прибыли на Т-м отрезке времени, IT — инвестиции на Т-м отрезке времени, KT — основной капитал в конце Т-го отрезка времени, YT — национальный доход на Т-м отрезке времени (вместо этой переменной были взяты данные по кварталам показателя валового внутреннего продукта, его оценка проводится в текущих и сопоставимых ценах, а также может рассчитываться в постоянных ценах базового периода c пересчетом на основе дефлятора).
Уравнения функционирования
Тождества
Случайные возмущения m1, m2, m3распределены по нормальному закону с математическими ожиданиями Еm1, Em2, Em3, равными нулю, и ковариационной матрицей
где через Переменные и управляющие воздействия, а также последние 3 тождества, которые были использованы Л. Клейном в этой модели для анализа экономики США в 60-х годах двадцатого столетия, как показали вычисления по модели, не совсем подходят для экономики Алтайского края. Нами были выбраны следующие переменные, приведенные в таблице 1 в текущих ценах. В расчетах они были разбиты по кварталам и были пересчитаны на основе дефлятора. По поводу данных, приведенных в таблице 1, и их использования в модели необходимо заметить следующее. 1) ФЗП органов управления – будет далее в модели выступать в качестве W2t (правительственный фонд заработной платы). В состав фонда заработной платы включаются начисленные предприятием, учреждением, организацией суммы оплаты труда в денежной и натуральной формах за отработанное и неотработанное время, стимулирующие доплаты и надбавки, компенсационные выплаты, связанные с режимом работы и условиями труда, премии и единовременные поощрительные выплаты, а также выплаты на питание, жилье, топливо, носящие регулярный характер. 2) Основные фонды (основные средства, основной капитал) – часть национального богатства, созданная в процессе производства, которая длительное время неоднократно или постоянно в неизменной натурально-вещественной форме используется в экономике, постепенно перенося свою стоимость на создаваемые продукты и услуги. В практике учета и статистики к основным фондам относят объекты со сроком службы не менее года и стоимостью выше определенной величины, устанавливаемой в зависимости от динамики цен на продукцию фондообразующих отраслей. Источниками информации об основных фондах служат формы статистической отчетности (формы № 11, 11 – краткая и др.), а также составляемые на их основе органами государственной статистики балансы основных фондов. В модели далее будет выступать в качестве Kt. 3) Инвестиции – денежные средства, целевые банковские вклады, паи, акции и другие ценные бумаги, технологии, машины, оборудование, лицензии, в том числе и на товарные знаки, кредиты, любое другое имущество или имущественные права, интеллектуальные ценности, вкладываемые в объекты предпринимательской и других видов деятельности в целях получения прибыли (дохода) и достижения положительного социального эффекта. В модели далее объем инвестиций будет выступать в качестве It. 4) Расходы на личное потребление - включают расходы домашних хозяйств на приобретение товаров и услуг во всех торговых предприятиях, на городских рынках и через неорганизованную (уличную) торговлю, предприятиях бытового обслуживания, пассажирского транспорта, связи, гостиницах, платных учреждениях культуры, здравоохранения, образования, а также потребление товаров и услуг в натуральной форме – произведенных для себя (сельскохозяйственная продукция личных подсобных хозяйств, условно исчисленные услуги по проживанию в собственном жилище) и полученных в качестве оплаты труда. В модели эти расходы на потребление будут выступать в качестве Ct. 5) Валовой региональный продукт (ВРП), представляет собой конечный результат производственной деятельности резидентных единиц-производителей в течение данного периода времени и исчисляется в рыночных ценах. Он предназначен для характеристики взаимосвязанных аспектов экономического процесса: производства товаров и оказания услуг, распределения доходов, конечного использования товаров и услуг. В зависимости от направлений исследования показателя валового внутреннего продукта его оценка проводится в текущих и сопоставимых ценах, а также может рассчитываться в постоянных ценах базового периода. Далее в модели валовой региональный продукт будет выступать в качестве Yt. 6) Валовая (чистая) прибыль представляет собой ту часть добавленной стоимости, которая остается у производителей после вычета расходов, связанных с оплатой труда наемных работников, и чистых налогов на производство и импорт. В модели далее объем прибыли будет выступать в качестве Пt. 7) Государственный заказ - заказ на покупку товаров, оказание услуг, проведение НИОКР, выдаваемый от имени органов государственного управления, финансируемый из государственного бюджета и направленный на удовлетворение общегосударственных нужд. Выдается, как правило, на условиях конкурса. В модели далее объем правительственных заказов будет выступать в качестве Gt. 8) Налог на прибыль – согласно российскому законодательству уплачивают юридические лица, осуществляющие предпринимательскую деятельность, а также филиалы и другие аналогичные подразделения предприятий, при условии, что они имеют отдельный баланс и расчетный счет. Объектом налогообложения является валовая прибыль, уменьшенная (увеличенная) в соответствии с положениями, установленными налоговым законодательством. В модели далее объем поступлений от налогов на прибыль будет выступать в качестве TXt. 9) Заработная плата в частном секторе – это заработная плата работников в частных предприятиях, показанная ими в соответствующих документах, подаваемых в налоговые органы. В связи с ее очевидным фактическим занижением в расчетах мы увеличили официальную величину в 3 раза. Далее будет выступать в качестве W1t. Оценка параметров Параметры уравнений функционирования рассматриваемой модели были оценены по двухшаговому методу наименьших квадратов. С учетом расчетов и замечаний эти уравнения имеют вид
Ковариационную матрицу можно оценить по формуле
Здесь через
|


 Совокупность случайных величин {2;у} считается заданной, если при числе заявок к > 1 определена совместная функция распределения вида
Совокупность случайных величин {2;у} считается заданной, если при числе заявок к > 1 определена совместная функция распределения вида

 может быть представлена в виде
может быть представлена в виде

 случайной величины
случайной величины 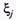 при j > 1 равно
при j > 1 равно




 — среднее число заявок, поступивших на обслуживание за интервал t,
— среднее число заявок, поступивших на обслуживание за интервал t, 
 — интенсивность или плотность потока.
— интенсивность или плотность потока.

 поток можно считать пуассоновским.
поток можно считать пуассоновским.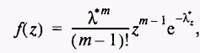




 , системы с ожиданием
, системы с ожиданием  и системы с ограниченным ожиданием
и системы с ограниченным ожиданием  Величина /ож — один из показателей качества СМО.
Величина /ож — один из показателей качества СМО.
 — интенсивность обслуживания одного требования одним обслуживающим устройством, а
— интенсивность обслуживания одного требования одним обслуживающим устройством, а


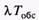 показывает число требований, поступающих в СМО за время обслуживания одного требования одним устройством. В этом случае число обслуживающих устройств п должно быть не меньше коэффициента загрузки, т.е.
показывает число требований, поступающих в СМО за время обслуживания одного требования одним устройством. В этом случае число обслуживающих устройств п должно быть не меньше коэффициента загрузки, т.е.









 зак/день и
зак/день и  зак/день характеристики качества обслуживания будут различными. Учитывая, что среднее число заявок, обслуживаемых в
зак/день характеристики качества обслуживания будут различными. Учитывая, что среднее число заявок, обслуживаемых в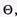 равногде
равногде  — среднее время об-
— среднее время об- одной машиной химчистки, причем
одной машиной химчистки, причем  суток, вычислим коэффициент интенсивности нагрузки
суток, вычислим коэффициент интенсивности нагрузки 2. Величина а характеризует среднее
2. Величина а характеризует среднее где п — число машин химчист-
где п — число машин химчист- а
а 
 зак/день очередь будет безгранично расти.
зак/день очередь будет безгранично расти.
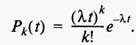
 и
и  таким образом, чтобы значение скорректированного потока
таким образом, чтобы значение скорректированного потока  ') зависело от месяца
') зависело от месяца  , дня
, дня  недели
недели  и времени суток
и времени суток  т.е.:
т.е.:


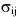 обозначено математическое ожидание произведения возмущений в i-м и j-м уравнениях, взятых в один момент времени (i, j= 1, 2, 3).
обозначено математическое ожидание произведения возмущений в i-м и j-м уравнениях, взятых в один момент времени (i, j= 1, 2, 3).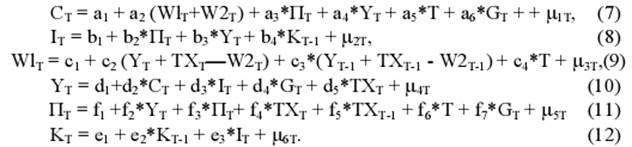

 обозначена матрица невязок уравнений, получающаяся при подстановке в систему (6) - (8) фактических данных, на основе которых найдены оценки параметров модели. Это матрица размера NxМ, где N — число наблюдений в исходной выборке, а М - число уравнений.
обозначена матрица невязок уравнений, получающаяся при подстановке в систему (6) - (8) фактических данных, на основе которых найдены оценки параметров модели. Это матрица размера NxМ, где N — число наблюдений в исходной выборке, а М - число уравнений.


