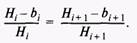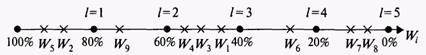Многокритериальные целевые функции распределения ресурсов
Существует множество задач, в которых требуется распределить какие-либо ресурсы, например капиталовложения, энергоресурсы, лимиты, квоты и т.п. В постановочном плане все эти задачи примерно одинаковы с позиции используемых критериев. Меняется только содержательное описание этих критериев. Пусть имеются объекты, для которых необходимо распределить ресурсы вида R исходя из двух критериев: экономического и внеэкономического. В качестве экономического критерия могут быть прибыль, себестоимость, удельные приведенные и неприведенные затраты, фондоотдача, транспортные затраты и т.п. Внеэкономическими критериями могут быть социальный, политический, экологический и иные эффекты любой размерности. Экономический критерий обычно выражается в экстремальной форме (min, max), а внеэкономический задается показателем в цифровой форме. Например, пусть внеэкономический критерий есть показатель социальной эффективности потребления населением услуг (бытовых, коммунальных, банковских и т.п.) в форме потребности в услугах надушу населения. Обозначим через Нь Н2>...,Н„ нормативы потребления услуг на душу населения, где / — вид услуги, / = 1, и. Норматив задает определенное числовое значение потребности в той или иной услуге. Введем также показатель фактического потребления услуг на душу в виде ЬЬЬ2,--, Ь„, который фиксирует реальное потребление услуг. В этом случае показатель социальной эффективности вложения ресурсов в тот или иной вид услуг / можно задать в виде степени относительного недопотребления Не-
действительно, Hj - bf представляет собой степень недопотребления /-х услуг на душу, а величина относительно установленного норматива Н-г Для лучшего восприятия степень относительного недопотребления выражается в процентах. Показатель степени относительного недопотребления еще не является целевой функцией или критерием, это только показатель. Разумно потребовать, чтобы показатель недопотребления был одинаковым для всех видов услуг, так как это будет справедливо по отношению к установленным нормативам Я;. Для этого введем условие равенства степени относительного недопотребления для всех видов услуг, а именно:
Это условие является уже целевой функцией, которую можно назвать целевой функцией пропорционального развития. Если рассчитать показатель W-, по каждой услуге и проранжировать их по величине от больших до меньших значений, то получим ряд ранжированных показателей, фиксирующих приоритетность вложений по видам услуг. Если имеем некоторую величину ресурса вложения, например капиталовложения, то его нужно вкладывать в первую очередь в те услуги, у которых значение Wt больше. На практике значения Wt для различных услуг могут быть близкими или даже одинаковыми, поэтому весь ранжированный ряд показателей W-, разбивается на интервалы, внутри которых показатели Щ признаются одинаковыми. Пусть Й4, W2,...,РИ",...,И^—■ ряд ранжированных показателей Щ, т = I, к, где к — число интервалов, на которые разбивается ранжированный ряд. Значение каждого интервала может меняться от 0 до 100%, т.е. если интервал равен 0, то имеем просто ранжированный ряд, где каждое значение Wj имеет свой ранг /. Если интервал равен, например, 20%, то в него попадают все значения Wh имеющие соответствующее близкое значение (рис. 9.13). На рис. 2.2.1 крестиками показаны значения соответствующих Wt для 9 видов услуг (и = 9) при интервале разбиения ранжированного ряда 20%. Для данного примера первый приоритет (ранг / = 1) имеют услуги с номерами 5 и 2, второй приоритет (ранг / = 2) имеет услуга 9 и т.п.
Рис. 9.13. Пример ранжирования показателей с шагом приоритета 20% При увеличении величины интервала число видов услуг, попадающих в каждый интервал, увеличивается, следовательно, внутри интервалов эти виды услуг считаются равноприоритетными. Если интервал равен 100%, то все услуги попадают в него и считаются равноприоритетными. Для услуг, попавших в один и тот же интервал, также осуществляется ранжирование, но уже по другому критерию, например экономическому. В частности, для рассматриваемого примера в качестве экономического критерия можно выбрать показатель удельных капиталовложений для каждого вида услуг. Например, для / = 1 в первую очередь выделяются ресурсы для той из услуг 2 или 5, у которой меньше удельные капиталовложения. Так же поступают по всем оставшимся интервалам ранжированного ряда. Если ресурсов хватает для всех 9 видов услуг, то их выделяют на все эти виды. В этом случае задачи оптимизации нет. Однако, как правило, ресурсов хватает далеко не на все виды услуг. В этом случае возникает задача оптимизации распределения ресурсов, и ресурсы выделяются только на те виды услуг, которые попадают по социальному приоритету в соответствующие первые ранги и по экономическому приоритету для последнего ранга, обеспеченного ресурсами. Это означает, что для последнего ранга, который обеспечивается ресурсами, последовательность выдачи ресурсов определяется величиной удельных капиталовложений. Чем они меньше, тем выше ранг этой услуги по экономическому критерию, и, следовательно, эта услуга насыщается ресурсами в первую очередь. Таким образом, выше сформулирована, по крайней мере, двух-критериальная задача, обеспечивающая пропорциональность развития объектов с максимизацией использования распределяемых ресурсов. Данная задача сформулирована в виде простой имитационной процедуры, которая позволяет осуществлять оптимизацию по двум критериям. Причем собственно имитационная модель, вычисляющая те или иные параметры, здесь еще не построена. Характерная особенность формирования данной двухкритериальной целевой функции состоит в том, что целевая функция генерируется имитационной процедурой,что является специфической особенностью имитационного подхода к моделированию. Данная имитационная процедура позволяет варьировать степень предпочтения между экономическим и внеэкономическим критериями за счет изменения шага приоритета для ранжированного ряда значений Wt. При шаге приоритета 100% внеэкономический критерий не действует, как при шаге 0% не действует экономический критерий. Меняя шаг приоритета, можно подобрать наиболее приемлемую для конкретного объекта модель распределения ресурсов.
|

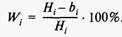
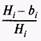 — степень недопотребления
— степень недопотребления