Оператор сопряжения
Под пространством сигналов или состояний понимается ‑ n -мерное векторное пространство типа
Точка в пространстве соответствует конкретному значению сигнала или состояния. Так, если задано пространство состояний Частные случаи пространств сигналов и состояний — двух- и трехмерное пространства. Наиболее наглядно двумерное пространство. На рис. 9.3 показано задание состояния некоторой системы в пространстве состояний. Последовательность состояний системы в различные моменты времени t1 t2,..., tn называется траекторией движения системы,которая показывает изменение состояния системы во времени. Реакция системы на какой-либо входной сигнал называется переходным процессом. Понятие переходного процесса можно применять как для состояний, так и для выходов системы. Поскольку при моде лировании нас интересует значение выходов системы, то чаще переходный процесс системы относят к выходным сигналам. Переходные процессы систем изображены на рис. 9.4. Эти процессы характеризуются временем переходного процесса Т, величиной перерегулирования Система называется устойчивой,если под действием входного сигнала она переходит из одного состояния равновесия в другое. На рис. 9.4 переходные процессы I и II соответствуют устойчивой системе, а III — неустойчивой. Как правило, все системы, которые подлежат моделированию, устойчивы.
Рис. 9.3. Пространство состояния системы
Рис. 9.4. Переходные процессы систем
|



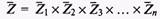 , где
, где  — ось пространства, то задание конкретного состояния системы означает задание точки
— ось пространства, то задание конкретного состояния системы означает задание точки  в пространстве состояний ее координатами. Координатами точки Z в пространстве
в пространстве состояний ее координатами. Координатами точки Z в пространстве  являются проекции этой точки на все оси пространства, т.е.
являются проекции этой точки на все оси пространства, т.е. 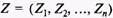 .
. (максимальное отклонение от Yo за время переходного процесса), величиной колебательности переходного процесса
(максимальное отклонение от Yo за время переходного процесса), величиной колебательности переходного процесса  (коэффициент демпфирования) и т.п. Переходный процесс — это показатель функционирования системы во времени,указывающий, как быстро и в какое новое состояние перейдет система в результате появления входного сигнала. Система находится в равновесии,если ее состояние может оставаться неизменным неограниченное время. В системе может быть несколько состояний равновесия. Она может переходить из одного состояния равновесия в другое под действием входных сигналов или внутренних причин.
(коэффициент демпфирования) и т.п. Переходный процесс — это показатель функционирования системы во времени,указывающий, как быстро и в какое новое состояние перейдет система в результате появления входного сигнала. Система находится в равновесии,если ее состояние может оставаться неизменным неограниченное время. В системе может быть несколько состояний равновесия. Она может переходить из одного состояния равновесия в другое под действием входных сигналов или внутренних причин.




