Модели AR(M).
Построим модели авторегрессии AR(M) = ARMA(M, 0) порядков M = 1, 2, 3.
Здесь Коэффициенты для данной модели найдем из системы уравнений Юла–Уокера. Для модели AR(3):
Для модели AR(2):
Для модели AR(1):
где Найденные коэффициенты моделей AR(M) запишем в таблицу 2. Таблица 2 – коэффициенты моделей AR(M)
Здесь же проверим устойчивость полученных моделей AR(М) · модель ARMA (0,N) = MA (N) устойчива всегда, · модель ARMA (1,N) устойчива только, если · модель ARMA (2,N) устойчива только, если · модель ARMA (3,N) устойчива только, если
Проведя расчеты, было выяснено, все модели являются устойчивыми.
Теперь найдем первые 10 теоретических значений НКФ для полученных моделей AR(M).
Таблица - 3 теоретические НКФ.
Погрешность модели мы считали по следующей формуле: Здесь Таким образом видим, что среди всех моделей AR(M) лучшая модель AR(2).
|
– значение k-ого элемента выходной последовательности модели авторегрессии M-ого порядка, 
, 
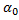– коэффициенты системы уравнений, 
- входная некоррелированная случайная последовательность с нулевым математическим ожиданием и единичной дисперсией.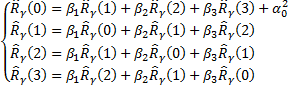
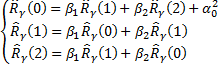
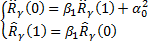
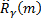– значения корреляционной функции в точке 
.
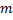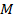
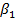
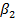
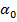
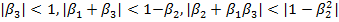
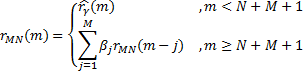
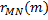
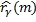
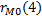
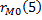
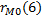
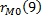
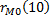
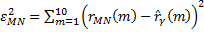
– это выборочная нормированная корреляционная функция, а 
– подсчитанная теоретическая корреляционная функция.
