КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Гауссовы пучки - очень важный для практики случай, встречающийся во многих естественных процессах
Гауссовы пучки - очень важный для практики случай, встречающийся во многих естественных процессах. Фундаментальный характер гауссовых пучков объясняется двумя основными свойствами - наименьшей расходимостью гауссова пучка и свойством сохранения гауссова распределения амплитуды при распространении в свободном пространстве. Благодаря этим свойствам поперечное распределение амплитуды света в луче лазера имеет гауссов вид. Резонатор лазера, как правило, образован двумя зеркалами, расположенными друг против друга. В процессе последовательных отражений происходит многократная дифракция на апертурах зеркал и большая часть дифрагировавшего света не проходит следующую апертуру. Таким образом, в результате многократной дифракции формируется пучок, наилучший с точки зрения расходимости. Кроме того, функция Гаусса - единственная, инвариантная к преобразованию Фурье, поэтому распределение амплитуды в дальней зоне дифракции также будет иметь гауссов вид. Рассмотрим распространение в свободном пространстве пучка с распределением амплитуды:
где
Рис.2.1. Распространение гауссова пучка в свободном пространстве Волновой фронт пучка в плоскости
где Основная энергия гауссова пучка сосредоточена в пятне радиуса
где z - координата вдоль оптической оси (рис. 2.1). Новый радиус гауссова пучка в дальней зоне
Таким образом, чем меньше радиус исходного пучка, тем больше его расходимость. Поскольку бесконечно удаленный наблюдатель видит исходный пучок как точку, волновой фронт на большом удалении сферический с радиусом кривизны Можно показать, что и в процессе распространения от плоскости перетяжки до дальней зоны пучок остается гауссовым. При этом происходит как изменение радиуса пучка
Как видно, в них присутствует параметр Важным для практики является преобразование гауссова пучка линзой. Идеальная тонкая линза преобразует только радиус кривизны пучка, оставляя его гауссовым. Действительно, плоская волна фокусируется линзой на расстоянии F, равном ее фокусу. Значит, плоская волна становится после линзы сферической с радиусом кривизны F. Следовательно, линза изменяет кривизну волнового фронта на величину 1/ F и новый радиус кривизны R связан со старым R 0 соотношением
При Рассмотрим важный для практики случай, когда линза расположена на большом удалении от перетяжки исходного пучка, радиус кривизны его в этом случае Если представить теперь на рис.2.1 линзу справа и предположить, что
где Для проверки параметров гауссова пучка, полученных путем измерений, следует вычислить
где L ‑ длина резонатора лазера, k ‑ волновое число.
|

 , (2.1)
, (2.1) ‑ амплитуда в начале координат;
‑ амплитуда в начале координат;  ,
,  ‑ система координат;
‑ система координат; 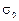 ‑ ширина распределения по уровню
‑ ширина распределения по уровню  (рис.2.1).
(рис.2.1).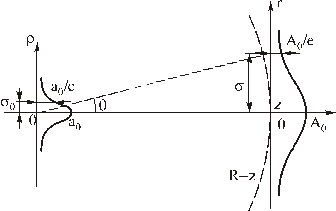
 ‑ плоский. Следует отметить, что при распространении гауссова пучка в свободном пространстве такая плоскость - единственная. Ее положение определяет место так называемой перетяжки гауссова пучка. Ширина пучка
‑ плоский. Следует отметить, что при распространении гауссова пучка в свободном пространстве такая плоскость - единственная. Ее положение определяет место так называемой перетяжки гауссова пучка. Ширина пучка  ,
,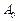 ‑ новая амплитуда в начале координат;
‑ новая амплитуда в начале координат; 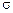 ‑ новый радиус луча.
‑ новый радиус луча. , следовательно угловая расходимость исходного пучка, измеренная в дальней зоне дифракции (там, где наблюдатель видит исходный пучок как точку), может быть выражена как при дифракции на отверстии радиуса
, следовательно угловая расходимость исходного пучка, измеренная в дальней зоне дифракции (там, где наблюдатель видит исходный пучок как точку), может быть выражена как при дифракции на отверстии радиуса  .
. , (2.2)
, (2.2) . (2.3)
. (2.3) (рис. 2.1).
(рис. 2.1). до значений (2.3), так и изменение волнового фронта пучка от плоского до сферического с радиусом
до значений (2.3), так и изменение волнового фронта пучка от плоского до сферического с радиусом  ,
, . (2.4)
. (2.4) , имеющий размерность длины и называемый конфокальным параметром гауссова пучка. Именно этот параметр и определяет границу дальней зоны дифракции для гауссова пучка. Условие дальней зоны -
, имеющий размерность длины и называемый конфокальным параметром гауссова пучка. Именно этот параметр и определяет границу дальней зоны дифракции для гауссова пучка. Условие дальней зоны -  . Легко видеть, что при этом (2.4) переходит в (2.3) и
. Легко видеть, что при этом (2.4) переходит в (2.3) и 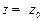
 .
. .
. после линзы
после линзы  , т.е. кривизна волнового фронта имеет другой знак, и мы получаем сходящийся гауссов пучок, который далее вновь образует перетяжку.
, т.е. кривизна волнового фронта имеет другой знак, и мы получаем сходящийся гауссов пучок, который далее вновь образует перетяжку.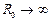 , т.е. волновой фронт фокусируемого пучка стремится к плоскому. После прохождения линзы радиус кривизны R будет равен F.
, т.е. волновой фронт фокусируемого пучка стремится к плоскому. После прохождения линзы радиус кривизны R будет равен F. , то фактически
, то фактически  и в соответствии с (2.3) мы получаем
и в соответствии с (2.3) мы получаем , (2.5)
, (2.5) , и радиус кривизны R на зеркале также равен
, и радиус кривизны R на зеркале также равен  легко получить
легко получить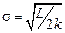 , (2.6)
, (2.6)


