КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Разрешающая способность - свойства оптической системы передавать мелкие детали изображения, т.е
Разрешающая способность - свойства оптической системы передавать мелкие детали изображения, т.е. раздельно воспроизводить близкорасположенные точки. Разрешающая способность оптической системы зависит от минимального размера изображения точки, cоздаваемого системой. Пусть на вход оптической системы подан предмет, состоящий из одной точки
Тогда на выходе получится некоторое световое поле вокруг сопряженной точки в плоскости изображения. Координаты этой точки равны Разрешение определяется шириной функции На практике расстояние до первого минимума можно измерить, наблюдая изображение точки через микроскоп с измерительной сеткой. Измерение ФРТ можно осуществить путем сканирования изображения точки фотоприемником с малым размером фоточувствительного элемента.
Рис. 2.7. Критерий Рэлея Однако для хороших высокоразрешающих систем, у которых δ ~ 1…5 мкм, такое измерение становится затруднительным в силу малой чувствительности или отсутствия фотоприемников с субмикронным размером фоточувствительного элемента. На практике более простым является другой метод получения информации о ФРТ, так называемый пограничный тест. Функция, описывающая спад интенсивности в изображении края полуплоскости, называется пограничной кривой. Количественная связь пограничной кривой с ФРТ дается соотношениями:
Пограничная кривая может быть получена сканированием изображения края полуплоскости точечным фотоприемником. Однако по указанным выше причинам эта процедура на практике не применяется. Но, как легко видеть, ее можно заменить сканированием изображения точки краем полуплоскости, т.е. измеряя изменение общего светового потока при передвижении непрозрачного ножа в плоскости изображения точки, создаваемого оптической системой. Этот тест легко осуществим на практике, так как существующие механические подвижки обеспечивают точность позиционирования 0,2…1,0 мкм. Измерение ФРТ, однако, не дает полной информации о разрешающей способности, поскольку реальные оптические системы не являются изопланатическими. Более приближенным к реальным условиям является визуальное определение разрешающей способности по штриховым или радиальным мирам. Штриховая мира – это набор изображений решеток с известным количеством штрихов на миллиметр. Разглядывая изображения мир под микроскопом, определяют максимальное число штрихов на миллиметр, которое разрешает данная оптическая система. Как правило, разрешающая способность системы различна на краях и в центре поля изображения. На краях она всегда меньше. Метод с использованием мир достаточно прост, однако основной его недостаток – зависимость результатов измерений от освещенности и физиологических данных оператора. Наиболее универсальной характеристикой оптической системы является ее передаточная функция (ПФ)
Рис 2.8. Определение разрешения через ЧКХ В данной работе используется упрощенный метод вычисления ОПФ по данным измерения пограничной кривой. Он основан на связи пограничной кривой с одномерным сечением ФРТ через производную (2.16). После численного дифференцирования пограничной кривой, применяя преобразование Фурье к полученной последовательности отсчетов ФРТ, можно получить одномерную ОПФ для какой-то определенной ориентации вектора При построении кривой ЧКХ следует помнить о связи цифрового Быстрого Преобразования Фурье (БПФ) и аналогового оптического ПФ. Первое важное отличие – в расположении начала координат пространственных частот (рис. 2.9).
Рис. 2.9. Вид спектра, полученного после БПФ В последовательности, полученной путем БПФ, максимальной частоте соответствует середина полученной последовательности отсчетов, то есть отсчет с номером N/ 2. Нулевой частоте соответствует начальный элемент последовательности. Таким образом, для получения ЧКХ в виде, как на рис.2.8, все элементы последовательности с номерами больше N/ 2, соответствующие отрицательным пространственным частотам, должны быть отброшены. При необходимости следует дополнить исходную последовательность, описывающую ФРТ, нулями до ближайшей степени двойки. Кроме того, интервал дискретизации БПФ по частоте n определяется как
|

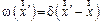 . (2.14)
. (2.14) . Комплексная амплитуда изображения
. Комплексная амплитуда изображения 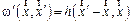 , т.е. изображение точки, рассеивается в пятно вокруг
, т.е. изображение точки, рассеивается в пятно вокруг  с интенсивностью
с интенсивностью  , называемой функцией рассеяния точки (ФРТ). Оптическая система называется изопланатической (пространственно - инвариантной), если вид функции h не зависит от положения точки
, называемой функцией рассеяния точки (ФРТ). Оптическая система называется изопланатической (пространственно - инвариантной), если вид функции h не зависит от положения точки 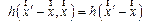 . Функция
. Функция 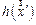 характеризует импульсный отклик на точечный предмет в точке
характеризует импульсный отклик на точечный предмет в точке 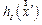 =
= 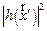 . Рассмотрим, как определяется разрешение по Рэлею (рис.2.7). Величина разрешения δ определяется как расстояние между двумя точками. Пунктиром на рис.2.7 изображены hI для двух близкорасположенных точек, а сплошной линией - суммарная интенсивность. Расстояние δ определяется, когда центральный максимум ФРТ одной точки совпадает с первым минимумом ФРТ другой точки. Провал в суммарной интенсивности при этом e = 0,225 от максимума интенсивности.
. Рассмотрим, как определяется разрешение по Рэлею (рис.2.7). Величина разрешения δ определяется как расстояние между двумя точками. Пунктиром на рис.2.7 изображены hI для двух близкорасположенных точек, а сплошной линией - суммарная интенсивность. Расстояние δ определяется, когда центральный максимум ФРТ одной точки совпадает с первым минимумом ФРТ другой точки. Провал в суммарной интенсивности при этом e = 0,225 от максимума интенсивности.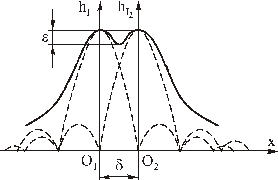
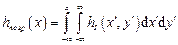 , (2.15)
, (2.15)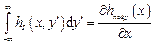 . (2.16)
. (2.16)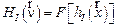 (некогерентная). Нормированная ПФ
(некогерентная). Нормированная ПФ 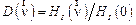 называется оптической передаточной функцией (ОПФ). ОПФ описывает преобразование оптической системой синусоидальной миры, причем
называется оптической передаточной функцией (ОПФ). ОПФ описывает преобразование оптической системой синусоидальной миры, причем 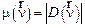 численно равна коэффициенту передачи контраста миры в зависимости от пространственной частоты
численно равна коэффициенту передачи контраста миры в зависимости от пространственной частоты 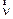 и называется частотно-контрастной характеристикой (ЧКХ) или функцией передачи модуляции (ФПМ), а
и называется частотно-контрастной характеристикой (ЧКХ) или функцией передачи модуляции (ФПМ), а 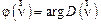 численно равна добавке к фазе миры в зависимости от пространственной частоты
численно равна добавке к фазе миры в зависимости от пространственной частоты 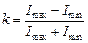 , где Imax, Imin – соответственно максимальное и минимальное значения интенсивности в изображении. Если теперь вспомнить, что представление изображения через преобразование Фурье можно интерпретировать как суммирование различных пространственных частот с комплексными коэффициентами, равными значениям спектра для этих пространственных частот, то становится ясным, что ОПФ является наиболее наглядной и универсальной характеристикой оптической системы, определяющей прохождение через нее различных пространственных частот. После введения понятия ОПФ очевидно, что нельзя говорить о разрешающей способности вообще, а только на каком-то уровне контрастности. Эти данные можно получить, имея график ЧКХ (рис. 2.8). Задавшись каким-то определенным значением потери контраста, скажем 0,5, по графику находят соответствующее ему значение разрешающей способности δ = 1/n0. Критерий Рэлея, таким образом, определяет разрешением системы на уровне контраста 0,225. Следует заметить, что контрастная чувствительность глаза при определенных условиях может достигать 0,05, то есть разрешение, определяемое визуально, может значительно превышать рэлеевское.
, где Imax, Imin – соответственно максимальное и минимальное значения интенсивности в изображении. Если теперь вспомнить, что представление изображения через преобразование Фурье можно интерпретировать как суммирование различных пространственных частот с комплексными коэффициентами, равными значениям спектра для этих пространственных частот, то становится ясным, что ОПФ является наиболее наглядной и универсальной характеристикой оптической системы, определяющей прохождение через нее различных пространственных частот. После введения понятия ОПФ очевидно, что нельзя говорить о разрешающей способности вообще, а только на каком-то уровне контрастности. Эти данные можно получить, имея график ЧКХ (рис. 2.8). Задавшись каким-то определенным значением потери контраста, скажем 0,5, по графику находят соответствующее ему значение разрешающей способности δ = 1/n0. Критерий Рэлея, таким образом, определяет разрешением системы на уровне контраста 0,225. Следует заметить, что контрастная чувствительность глаза при определенных условиях может достигать 0,05, то есть разрешение, определяемое визуально, может значительно превышать рэлеевское.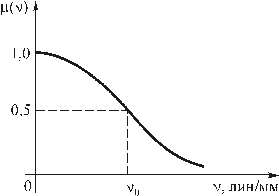
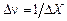 , D X – область измерения кривой ФРТ. Поскольку из-за добавления нулей в последовательность, описывающую ФРТ, не всегда удобно рассчитывать D X, можно воспользоваться другим соотношением:
, D X – область измерения кривой ФРТ. Поскольку из-за добавления нулей в последовательность, описывающую ФРТ, не всегда удобно рассчитывать D X, можно воспользоваться другим соотношением: 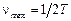 , где
, где 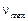 -максимальная частота, соответствующая отсчету спектра с номером N/ 2, а T ‑ шаг дискретизации пограничной кривой. Таким образом, при T =0,005 мм (5 мкм), максимальная анализируемая частота составит 100 лин/мм, что вполне достаточно для исследования большинства оптических систем среднего качества.
-максимальная частота, соответствующая отсчету спектра с номером N/ 2, а T ‑ шаг дискретизации пограничной кривой. Таким образом, при T =0,005 мм (5 мкм), максимальная анализируемая частота составит 100 лин/мм, что вполне достаточно для исследования большинства оптических систем среднего качества.


