КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Дифракционные оптические элементы (ДОЭ) представляют собой прозрачную подложку с нанесенным на нее микрорельефом
Дифракционные оптические элементы (ДОЭ) представляют собой прозрачную подложку с нанесенным на нее микрорельефом, разность хода лучей на котором обычно не превышает λ. Для сравнения – разность хода для обычных рефракционных элементов (линз, призм) составляет тысячи и даже десятки тысяч λ. Фазовый рельеф рассчитывается на компьютере и реализуется с помощью специальных прецизионных устройств. Такие элементы позволяют решать новые классы задач в оптике. Одной из таких задач является формирование заданного распределения интенсивности в фокальной области. Такая задача может решаться также оптической системой, включающей ДОЭ и обычные рефракционные линзы. Линзы обеспечивают большую часть необходимой оптической силы, а ДОЭ нужным образом перераспределяют энергию в фокальной области. Один из подходов к расчету таких ДОЭ состоит в реализации некоторой периодической фазовой функции, то есть дифракционной решетки, у которой специальным образом рассчитывается фазовая функция. Будем понимать под спектром решетки распределение энергии в фокальной области при падении на решетку сходящейся сферической волны. Спектр решетки практически не зависит от поперечного распределения интенсивности в падающем на нее излучении. Данное свойство решеток является основным преимуществом по сравнению с другими ДОЭ, предназначенными для решения подобных задач. Классическая дифракционная решетка реализуется в виде периодической фазовой или амплитудной функции и характеризуется направлениями на главные максимумы. Получить непрерывную фокальную картину, например в виде линии, путем периодического повторения некоторой фазовой функции невозможно. Распад фокальной картины на пятна при наличии многих периодов физически обусловлен когерентной интерференцией световых полей, дифрагированных на разных периодах. Для решения задачи необходимо со сдвигом повторять фазовую функцию элемента, но при этом дополнительно вводить фазовые сдвиги таким образом, чтобы фокальная картина оставалась непрерывной. Таким образом согласуются фазовые функции периодов, то есть создается квазипериодическая структура. Покажем, как находить нужные величины фазовых сдвигов. Рассмотрим одиночный фокусирующий элемент с фазовой функцией f (x), где 0 <x<d. Для сходящегося лазерного пучка с равномерным распределением интенсивности в пучке фокальная картина описывается коэффициентами Фурье, соответствующими главным направлениям дифракции:
где F ‑ фокусное расстояние, u ‑ координата в фокальной плоскости. Распределение амплитуды c(u) полностью определяется величинами cn, то есть своими значениями в точках un, а между ними интерполируется sinc -функцией. Если повторить функцию f (x) с фазовыми сдвигами pk N раз, то период станет в N раз больше и каждый интервал
Если все pk =0, то это дает am = 0 при m, отличных от 0, то есть распад фокальной картины на пятна N. Но можно найти такие pk, что Весьма важный для практики случай – бинарно-фазовые решетки, фаза которых принимает лишь два значения. У них тоже можно управлять спектром путем модуляции фазовой функции. Модуляция осуществляется путем сложения двух бинарных решеток, период одной из которых значительно больше другой. При этом решетка остается бинарной. Рассмотрим две бинарные решетки с фазовыми функциями φ(x) и ψ(x) и периодами d и D соответственно. Сложению фазовых решеток соответствует произведение функций пропускания, и новая решетка будет иметь функцию пропускания
где am bk – коэффициенты ряда Фурье для первой и второй решеток соответственно. Данную формулу трудно использовать для построения решеток с конкретной формой спектра. Единственным исключением является построение решетки с большим количеством подряд идущих порядков одинаковой энергии и близкой к нулю энергией в остальных порядках. В общем случае требуется решать систему нелинейных уравнений, размерность которой определяется числом порядков равной энергии, что весьма сложно. Можно упростить задачу, положив D=nd. Если рассматривать D, как период (не минимальный) и для второй решетки, то ее спектр будет отличаться тем, что an =0 при При исследовании реальных ДОЭ, вследствие погрешностей изготовления, как правило, нулевой порядок дифракции превосходит по интенсивности остальные (см. рис 2.11). Кроме того, появляются высшие порядки дифракции, в которых периодически повторяется рассчитанный спектр с меньшей интенсивностью (см рис 2.11). Целью экспериментального исследования и является выделение нужных участков спектра и исследование полученного распределения интенсивности.
Рис. 2.11. Вид спектра при исследовании дифракционных решеток
|

 (2.17)
(2.17) разделится на N подынтервалов, при этом интерполирующая функция в точках, разделяющих эти интервалы, описывается дискретным преобразованием Фурье вида
разделится на N подынтервалов, при этом интерполирующая функция в точках, разделяющих эти интервалы, описывается дискретным преобразованием Фурье вида . (2.18)
. (2.18)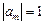 при m= 0, 1, 2, …, N- 1, то есть интенсивность фокальной картины
при m= 0, 1, 2, …, N- 1, то есть интенсивность фокальной картины  остается такой же, как и при наличии только одного периода. Интерференция пучков от разных периодов не исчезает, но в фокальной плоскости влияет лишь на фазу, а не на интенсивность.
остается такой же, как и при наличии только одного периода. Интерференция пучков от разных периодов не исчезает, но в фокальной плоскости влияет лишь на фазу, а не на интенсивность. . Положим сначала d = D. Тогда коэффициенты Фурье для новой решетки
. Положим сначала d = D. Тогда коэффициенты Фурье для новой решетки ,
,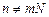 , то есть ненулевую энергию будет иметь только каждый N -й порядок дифракции, включая нулевой. Тогда выбрав в качестве второй решетки такую, что ее спектр имеет ровно N подряд идущих порядков одинаковой энергии, а энергия остальных близка к нулю, мы можем получить при условии, что первая решетка того же типа и имеет M равных по энергии порядков решетку, которая имеет NM близких по энергии порядков. Можно взять в качестве второй решетки снова первую, сжав ее период в N раз.
, то есть ненулевую энергию будет иметь только каждый N -й порядок дифракции, включая нулевой. Тогда выбрав в качестве второй решетки такую, что ее спектр имеет ровно N подряд идущих порядков одинаковой энергии, а энергия остальных близка к нулю, мы можем получить при условии, что первая решетка того же типа и имеет M равных по энергии порядков решетку, которая имеет NM близких по энергии порядков. Можно взять в качестве второй решетки снова первую, сжав ее период в N раз.



